La belleza oculta de la matemática
Compartimos 13 recursos que abordan la matemática desde distintos ángulos, visiones y disciplinas. En las matemáticas, hay amor, prolifera el arte, emergen patrones, hipnotiza la naturaleza, circulan objetos increíbles y se generan paradojas, entre otras atracciones. Lo más importante es que les proponemos lecturas, videos y actividades ¡sin fórmulas y con mucha imaginación!
¿La matemática puede ser más romántica que una película de Hollywood?
La matemática es más que números y fórmulas; también es amor, seducción y misterio. A veces genera objetos fascinantes y paradojales como la cinta de Moebius y otras asombra con los nudos de los zapatos y de los marineros. La topología puede parecer mágica; sin embargo, es una rama de la matemática. Los invitamos a dejarse hechizar con su ciencia.
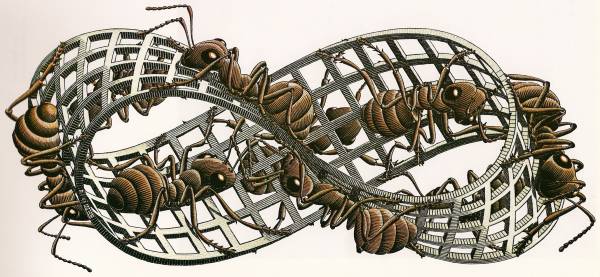
M. C. Escher: el cruce maravilloso del arte con el hechizo de la matemática
Escher atravesó el alma de la matemática por medio del arte para crear obras únicas. Dibujos, ensayos, desarrollos artísticos, pinturas, grabados... Toda la producción de este genial artista holandés señala —si estamos dispuestos a jugar, indagar y entregarnos a las paradojas— incitantes caminos de descubrimiento. ¿Y si ensayamos una nueva mirada y le tomamos el gusto a la otra matemática?

Figuras, objetos y dimensiones: cómo despegar de Planilandia
¿Cómo pensamos los objetos que amamos? ¿Queremos explorar las formas en que las neurociencias y la cultura ven el mundo a través de las imágenes y de las ideas? ¿Nos atraen las novelas geométricas y las esferas parlantes...? Entonces estamos listos para dar el paso a la cuarta dimensión. Nos acompañarán en este fascinante recorrido dos libros y una película.

¿Por qué no se caen los balcones? Al fin matemáticas sin fórmulas
El arquitecto y docente Mario Salvadori explicaba por qué los edificios permanecían de pie sin desplomarse. Lo más interesante es que lo hacía sin desplegar fórmulas terroríficas. La creatividad y la imaginación son las mejores aliadas de la matemática.

Las ilusiones ópticas de Escher impresas en 3D
No se trata de una ficción de Bradbury ni de Asimov; la impresión de objetos en tres dimensiones es un hecho. Más sorprendente aún es que una impresora 3D sea capaz de generar las estructuras imposibles del artista M. C. Escher.

El número pi: la matemática de todas las cosas
El número pi es una constante matemática. Y en esta actividad los invitamos a conocer una película en la que el protagonista supone que pi es un número mágico que todo lo gobierna.

Números, palíndromos y paradojas: otras maneras de contar
Un punto es lo que no puede dividirse, una línea es una longitud sin anchura... No podemos negar que estos son conceptos poéticos, así como lo son los palíndromos. Parece un buen ejercicio entonces intentar otra mirada para darnos cuenta de muchas cosas que pasan inadvertidas en la vida cotidiana y sobre todo las relaciones que esas cosas establecen entre sí: como la poesía y la matemática, como la narrativa y los números.
La matemática incrustada en la inmensa variedad de formas de vida
Subyace una matemática sutil detrás de todo cuanto nos rodea, desde el patrón de crecimiento de un helecho hasta el trino de las aves, la disposición de los pétalos en las flores, la estructura del caparazón de ciertos moluscos y la espiral de una galaxia en el universo, por nombrar solo algunos entre cientos de ejemplos. La llamada sucesión de Fibonacci es una de las formas matemáticas para encontrar el denominador común entre los patrones y los diseños de la naturaleza.

¿Las matemáticas se descubrieron o se inventaron?
Desde la antigüedad, la humanidad ha debatido acaloradamente sobre si las matemáticas se descubrieron o se inventaron. ¿Existirían las matemáticas si las personas no existieran? ¿Creamos conceptos matemáticos para entender el universo que nos rodea o las matemáticas son el lenguaje nativo del universo que existe aunque descubramos o no sus verdades?
La ecuación matemática escondida en las pinturas de Vincent van Gogh
Uno de los aspectos más extraordinarios del cerebro humano es su habilidad para reconocer patrones y describirlos. Entre los patrones más complicados de entender está el concepto de turbulencia en la dinámica de fluídos. Con su pintura “La noche estrellada” (1889), Vincent van Gogh se adelantó casi sesenta años al matemático Kolmogorov en el entendimiento intuitivo del fenómeno de la turbulencia. En este recurso les mostramos cómo el arte puede hacer ciencia.

Potencias de 10: ceros, átomos y el tamaño de todas las cosas
¿Qué efecto produce en un número agregar otro cero? ¿Cómo varía la cantidad o el tamaño al agregar o quitar un cero de una cifra? ¿Los átomos que componen a las hormigas y a los seres humanos pueden ser los mismos que constituyen a los planetas y a las galaxias, siendo que los tamaños y las complejidades son tan diferentes?

Geometría bajo el agua: arrecifes de coral versus Euclides
La geometría hiperbólica revolucionó las matemáticas cuando fue descubierta en el siglo XIX, pero se pensaba que sus estructuras eran imposibles de recrear. Los corales tuvieron la respuesta en su propia morfología durante aproximadamente 50 millones de años, pero no fue hasta 1997 que Daina Taimina -una matemática de la Universidad de Cornell, EE.UU- comprendió que ese tipo de estructuras ¡se podían tejer! En 2005, dos hermanas, Margaret y Christine Wertheim: una científica y una artista iniciaron un proyecto que consiste en tejer corales al crochet. Esos tejidos son estructuras hiperbólicas.

Aritmética vegetal para la supervivencia
La plantas tienen la capacidad de resolver problemas matemáticos que las ayudan a regular las reservas de alimentos durante la noche. Cuando la planta no puede utilizar la energía solar para convertir dióxido de carbono en azúcares y almidón, regula sus reservas de alimentos para garantizar que estos duren hasta el amanecer. A través de modelos matemáticos, los científicos pudieron demostrar que la cantidad de almidón consumida por las plantas durante la noche es calculada a partir de operaciones aritméticas de división muy específicas.

Ficha
Publicado: 04 de febrero de 2019
Última modificación: 16 de abril de 2025
Audiencia
Docentes
Estudiantes
Familias
Área / disciplina
Matemática
Nivel
Secundario
Superior
Categoría
Entrevistas, ponencia y exposición
Modalidad
Todas
Formato
Texto
Etiquetas
enseñanza de la matemática
arte
número pi
banda de Moebius
M. C. Escher
Autor/es
Carina Maguregui
Licencia
Creative Commons: Atribución – No Comercial – Compartir Igual (by-nc-sa)
