Las ilusiones ópticas de Escher impresas en 3D
No se trata de una ficción de Bradbury ni de Asimov; la impresión de objetos en tres dimensiones es un hecho. Más sorprendente aún es que una impresora 3D sea capaz de generar las estructuras imposibles del artista M.C. Escher.
Existen muchos relatos de ciencia ficción y filmes cuyas tramas fantásticas se llevaron a la pantalla y quedaron grabadas en las retinas de manera inolvidable. Algo más extraordinario aún ocurre cuando alguna de esas especulaciones se convierte en realidad. Dentro del terreno de lo posible, las creaciones e inventos del ser humano impactan en nuestras vidas de modos insospechados. Uno de los últimos desarrollos más interesantes son las impresoras para reproducir objetos en tres dimensiones.
Objetos a la carta
Con un material de base constituido por filamentos plásticos reciclables y el modelo de lo que se quiere imprimir cargado en la computadora, solo queda esperar unas horas para tener en las propias manos, por ejemplo, una escultura impresa. Se pueden imprimir todo tipo de objetos. Para llevar este desafío a un nivel mayor, Gershon Elber, investigador y profesor de informática en el Instituto de Tecnología de Israel, logró imprimir obras de M. C. Escher en 3D. Los objetos tridimensionales obtenidos por Elber, como el castilllo de Belvedere y la cascada de Escher, parecen haber resuelto la problemática espacial que planteó el mismo Escher originalmente, ya que al rotarlos se descubre el engranaje de su creación.
Impresora 3D. A partir del minuto 2, la impresora de Gelber en pleno funcionamiento
¿Quién fue M. C. Escher?
Hay muchas maneras de acercarse a la matemática, pero en general resultan aburridas o incomprensibles o, en cierta manera, producen frustación. A veces las personas se ven a sí mismas como improvisados Quijotes en el intento improbable de encontrarle la vuelta a los molinos de sus engranajes: vientos de fórmulas, geometrías que soplan desde los ángulos más inesperados y espeluznantes teoremas que amenazan con derribar a la gente de la montura del entendimiento. ¿Será que la matemática es en verdad una caja negra herméticamente cerrada cuyo misterio está negado descubrir? La respuesta es: no.
La matemática posee una belleza tan especial y extraordinaria que es necesario aproximarse a ella de modos no convencionales, sutiles, más desestructurados y lúdicos. A quienes así lo hicieron se les abrió una multiplicidad de mundos asombrosa. Una de las personas que atravesó el alma de la matemática a través del arte para crear obras únicas fue M. C. Escher. Los dibujos, los ensayos y desarrollos artísticos, las pinturas, los grabados y toda la producción del genial artista holandés señalan incitantes caminos de descubrimiento. Eso sí: hay que estar dispuestos a jugar, indagar, observar, investigar y entregarse a las paradojas.
¿Es posible ensayar una nueva mirada y tomarle el gusto a la otra matemática? Esa matemática despojada de los prejuicios y tabúes, la que está emparentada con todas las cosas de la vida cotidiana; la que se percibe, se usa y se practica todos los días intuitivamente sin saberlo.
M. C. Escher, el hombre al que todo lo asombraba
Escher observaba y hallaba patrones de diseño en el piso de un patio, en los árboles de un bosque, en la alineación de una bandada de pájaros que pasaba volando y en todos y cada uno de los detalles más comunes de la vida cotidiana. Porque para Escher era precisamente en la vida donde pasaban las cosas. A él no le interesaban las teorías, los ámbitos académicos ni las evaluaciones ni los currículums, ni los programas de las materias ni los ciclos escolares. A él le interesaba pescar la poesía de los patrones matemáticos con su lápiz / pincel / red.
Escher sintió con sus manos de artista inquieto qué significaba la fractalidad y fabricó hermosos caleidoscopios y teselaciones. Entendió estéticamente los atributos de los ángulos sin recitar como loro teoremas llenos de catetos. Ni hablar de comprender las dimensiones, los espacios y las transformaciones geométricas, de fabricar tablas de datos sabiendo lo que hacía, emocionándose al vislumbrar tendencias.
Tocó con su imaginación y sus creaciones —como si fueran instrumentos musicales— las repeticiones rítmicas de los patrones y de las metamorfosis. Combinó figuras geométricas, hizo miles de rotaciones, recreó paradojas de escaleras que suben y bajan al mismo tiempo. Manipuló objetos a su antojo y exploró los sólidos platónicos con la intuición y el plástico.
Existe un espejo mágico como el que vemos a continuación:
En el borde del espejo, inmediatamente debajo del listón torcido, vemos la punta de una pequeña ala y su reflejo. Si se mira a lo largo del espejo, se comprobará que se va transformando en un perro con alas y su reflejo. Una vez aceptada la posibilidad de semejantes alas, se acabará por creer el resto de la historia. Tan pronto como el perro real —a la derecha del espejo— se pone en marcha en esa misma dirección, su reflejo se moverá en la dirección opuesta. Sin embargo, el reflejo parece tan real que en nada sorprende verlo correr detrás del espejo. Perros con alas evolucionan a la derecha y a la izquierda y se duplican en el trayecto. Luego avanzan unos contra otros como dos ejércitos. Pero antes de encontrarse, se habrán convertido en motivos decorativos de un piso embaldosado.
Si se examinan de cerca estos motivos, se verá que los perros se vuelven blancos en el momento de cruzar el límite que forma el espejo, viniendo a ocupar los huecos existentes entre los perros que no han mudado de color. Los perros blancos desaparecen y al final no queda ningún rastro de ellos. Al parecer, nunca existieron. Después de todo nunca se han visto nacer perros voladores de un espejo. Pero... es un hecho que frente al espejo también hay una esfera, incluso se puede ver parte de su reflejo en el espejo. Y como si esto fuera poco, se ve claramente otra esfera detrás del espejo rodeada por perros alados.
¿Quién es el hombre que creó semejante espejo? ¿Se imaginan? Por supuesto, Escher.
El día y la noche según Escher...
Este grabado en madera de 1939 se considera uno de los dibujos más admirados y reproducidos del artista y es ciertamente bello por su sencillez y elegancia. Incluye varios detalles interesantes, como son la combinación en forma de patrón de pájaros blancos y negros que vuelan en direcciones opuestas y rellenan el plano sin huecos, la metamorfosis delicada pero rápida de las aves a sembrados en la escena general y el hecho de que las dos zonas, izquierda y derecha, una de día y la otra de noche, correspondan exactamente al mismo lugar. Un montón de dualidades genialmente resueltas en la misma escena.
Más matemático que artista
Maurits Cornelis Escher nació en Holanda en 1898 y en su juventud estudió en la Escuela de Arquitectura y Diseño Ornamental de la ciudad de Haarlem. A lo largo de su vida viajó por toda Europa y residió en Italia, Suiza y Bélgica. Murió en su país natal en 1972, momento en el que el reconocimiento de su obra comenzaba a adquirir carácter global. Hoy en día su obra es mundialmente conocida y aparece en multitud de lugares, desde camisetas a portadas de libros científicos. Gran cantidad de gente conoce los grabados y litografías de Escher, aunque muchos menos podrían señalar quién es su autor.
Video homenaje a la obra de Escher
El arte de Escher entra de lleno en el concepto de «arte matemático»: un artista figurativo que sepa algo de matemáticas puede hacer una composición sobre un tema matemático de la misma manera que los artistas del Renacimiento lo hicieron con los temas religiosos o los artistas rusos con los temas políticos.
Escher ha escrito: «Con frecuencia me siento más próximo a los matemáticos que a mis colegas los artistas». A pesar de ello, Escher no poseía estudios matemáticos extensos ni completos. Prefería decir: «Todos mis trabajos son juegos. Juegos serios». Sus obras cuelgan en los despachos de matemáticos y científicos de todo el mundo.
En muchos de sus trabajos podemos encontrar aspectos surrealistas, pero sus obras no son fantasías oníricas como las de Dalí o Magritte, son más bien observaciones filosóficas y racionales sobre el misterio, el absurdo y las paradojas.
Breve documental sobre Escher y su obra
Las teselaciones de los mosaicos escherianos
Una teselación es una regularidad o patrón de figuras que cubre o pavimenta completamente una superficie plana. Cumple con dos requisitos: que no queden huecos y que no se superpongan las figuras. Las teselaciones se crean usando transformaciones isométricas sobre una figura inicial.
Distintas culturas en el tiempo han utilizado esta técnica para formar pavimentos o muros de mosaicos en catedrales y palacios. Escher admiraba profundamente las teselaciones del complejo palaciego de la Alhambra, en Granada, España, y dedicó muchos años de su vida a la creación de diferentes series de teselaciones.
Sin duda la parte fundamental de la obra de Escher la constituye la división regular del plano. Era su principal obsesión y forma parte, de una u otra manera, de la mayoría de sus producciones. Desglosando el plano en figuras de pájaros, peces, reptiles y figuras humanas, como en un rompecabezas, Escher ha logrado incorporar muchas de sus divisiones del plano en composiciones memorables: los mosaicos escherianos.
Mundos imposibles
Otra de las categorías de las figuras de Escher, y sin duda aquella que sorprende más al que ve su obra por primera vez, está constituida por aquellas piezas en las que juega con las leyes de la perspectiva para obtener lo que se ha denominado mundos imposibles, imágenes que desafían la realidad tal como la conocemos y que la mente se niega a aceptar por mucho que las contemple.
Escena de la película Laberinto (1986) inspirada en los mundos imposibles de Escher
El espacio en el papel
Una de las obsesiones también presentes en muchas de las obras de Escher es la relación entre lo plano y lo espacial. Cuando alguien dibuja, lo hace sobre un medio plano, bidimensional, como es el papel. Pero lo utiliza para representar imágenes que son espaciales, tridimensionales. Escher juega con esta dualidad para crear algunas imágenes paradójicas absolutamente desconcertantes.
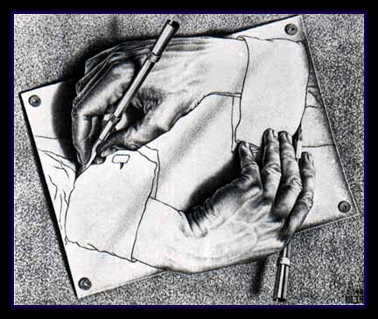
Por ejemplo, esta litografía de Escher de 1948 es tan sencilla como lo que se ve a simple vista: dos manos que surgen de la bidimensionalidad del papel a las tres dimensiones de la «realidad». Pero cada mano está dibujando a la otra, de modo que el efecto causa confusión en el observador. Irónicamente, ambas manos no están en tres dimensiones, ni existen por sí mismas, sino que habitan en un dibujo plano y fueron creadas por una única mano, mucho más experta, desde el exterior de la escena: la de M. C. Escher.
Entre los temas recurrentes de Escher se pueden citar también el orden y el caos, el infinito, las esferas reflectantes, las cintas de Moebius, lo cóncavo y lo convexo. Luego de ver y recorrer los paisajes escherianos, es recomendable leer algunos textos breves de Jorge Luis Borges en los que pueden hallarse y sondearse temas y conceptos que Escher ha plasmado en el papel: los laberintos, la circularidad, los mundos paralelos, etc.
El impactante efecto Droste
Esta litografía de 1956 era una de las obras de las que Escher estaba más orgulloso, aunque no es de las más conocidas. Es un juego a modo de ciclo con las perspectivas y las ampliaciones. Un hombre está mirando un cuadro. La imagen comienza a ampliarse y deformarse, pero manteniendo cierta coherencia visual que permite seguirla paso a paso sin interrupción aparente. El cuadro se transforma en los edificios del puerto de una ciudad costera —el puerto de Senglea, en Malta— uno de los cuales resulta ser una galería de cuadros donde vuelve a aparecer el protagonista. Se puede calcular que la imagen original queda ampliada 256 veces. En los detalles de la galería aparecen otros cuadros, pequeñas reproducciones de obras del propio Escher.
Galería de imágenes con efecto Droste
Los primeros pasos en un mundo increíble
Un dibujo, una litografía, una pintura no reflejan solo una imagen, sino que abren los mundos que llevan en su interior. Adentrarse en la obra de M. C. Escher puede brindar las herramientas necesarias para abrir esos mundos y disfrutarlos. Las emociones despertadas por las imágenes pueden iluminar la vida real y arrojar cierta claridad sobre la propia vida del que los contempla.
En esta litografía de 1943, Escher hace un salto de «metanivel» para introducir en el dibujo al propio autor como parte de la obra, todo ello frente a los ojos atónitos del espectador. Del cuaderno de Escher en el que ha estado dibujando patrones regulares hexagonales con forma de reptil surge una figura en tres dimensiones. El reptil sube por un libro, llega hasta un dodecaedro platónico, finalmente lanza un soplido y completa el ciclo retornando al papel del que nunca debió haber salido.
Instrucciones para fabricar un calidociclo

La publicidad de Audi A6 y M. C. Escher
Este es un enlace a una antigua pero interesante publicidad, el anuncio del auto Audi A6 basado en imágenes M. C. Escher, figuras imposibles y algunas variaciones de sus obras y otras escenas sorprendentes. Una bonita combinación artística y de efectos especiales.
Escher remix
La gente que fue seducida por el arte de Escher combina las ilustraciones originales del genial artista de las formas más diversas: dándoles color, mezclando unas con otras, ubicándolas en situaciones más imposibles todavía o modernizándolas un poco, como esta Mano con iPod, que es una variante de Mano con esfera reflectante.
Mano con iPod
Mano con esfera reflectante
El autorretrato de Escher sobre una esfera reflectante es precioso y a la vez intrigante. En esta obra vuelve a combinar el mundo imaginado del dibujo con el mundo real. Se dibuja a sí mismo sosteniendo una esfera, pero ese dibujo tridimensional que incluye su mano y la esfera-espejo es únicamente tinta sobre un papel plano. Al menos eso es lo que se ve. Aunque la esfera parece reflejar a Escher y la habitación que lo rodea con lujo de detalles, en realidad no lo muestra a Escher dibujando porque su mano izquierda está apartada.
Tal vez Escher está sugiriendo sutilmente que la realidad no es tal y como parece percibirse y que el mundo que nos rodea está a veces entre lo imaginario y lo real. Esto, que puede sonar un poco a Matrix, fue precisamente homenajeado en la famosa escena de la «pastilla roja, pastilla azul». En la película, mientras uno de los reflejos de las gafas de Morfeo muestra a Neo levantando la mano, en el otro tiene la mano apartada. Como ocurre con Escher en su autorretrato.
Actividades recomendadas
Luego de ver los materiales de Escher, la propuesta es elegir algunos dibujos. Cada estudiante observará detenidamente los dibujos y luego comentará su visión de las imágenes. Desde ya, esta actividad demostrará la pluralidad de puntos de vista porque cada individuo no responde de la misma manera que otro. Así surgirán discusiones muy interesantes sobre las variaciones. Suele haber una base de acuerdo general y distintas opiniones, comentarios e ideas sobre los componentes de la imagen, argumentaciones sobre cuáles de esos componentes llaman más la atención y las posibles razones de por qué capturan la mirada.
En Escaleras arriba y escaleras abajo, por ejemplo, unos monjes suben y bajan —a la vez— por la misma estructura del edificio sin que ninguno de los dos grupos parezca estar haciendo algo distinto a lo que realmente se ve. Sin embargo, ese ascenso o descenso infinito es claramente imposible, aunque el espectador no puede encontrar la inconsistencia por mucho que mire la imagen. ¿Qué sucedería de lanzar una pelota escaleras abajo? Esta idea está basada en el modelo de escalera imposible creado por Roger Penrose junto con su padre. Penrose es un físico y matemático británico que también exploró el mundo de los objetos imposibles y la partición regular e irregular del plano.
Modelo de guía optativa para ayudar en la observación/exploración de los diversos dibujos, litografías y diseños
- 1. Después de observar la imagen como un todo, volvé al punto de partida. ¿Por qué te dirigiste a ese punto en particular? Tratá de explicar qué hay allí que te indujo a detener tu mirada. (Las razones más comunes son las siguientes: es el punto de más luminosidad o es el lugar más oscuro de una composición o hay una zona de color muy llamativo o un determinado cruce de líneas o formas atraen la vista porque crean un punto focal).
- Cuando separaste la vista de este punto de atracción inicial ¿qué camino siguió tu mirada sobre la imagen? (Este desplazamiento sobre la imagen se produce, generalmente, a lo largo de líneas, quizás líneas reales como las de una cerca en la pintura o un brazo extendido en un dibujo o líneas de visión de un personaje que mira algo o alguien, etc. Hay ocasiones en que la vista se limita a desplazarse a otra área importante de la composición y va de un área organizada a otra saltando a través de la «desorganización» que existe entre medio).
- ¿Qué cantidad de movimiento hizo tu vista antes de volver a su punto de partida?
- ¿Qué es lo que atrajo tu vista a cada nuevo lugar de la imagen? (Los puntos 3 y 4 dan una idea de la fuerza de atracción que ejercen determinados elementos de la imagen).
- Si trazás una línea imaginaria sobre la imagen, según la ruta que siguió tu vista, ¿cuál sería la forma aproximada? (Hay veces que será un esquema circular; otras, un triángulo o una elipse. Aun cuando se pueden dar formas muy variadas, cualquiera de las formas nos puede servir de sugerencia para que organicemos la composición de una u otra manera y superar así la idea dominante y poco feliz de que cada imagen «dice obligatoriamente determinada historia»).
- ¿Hay algunos lugares de tu línea imaginaria que parecen estar cargados de una energía especial? (Este caso se da con mayor frecuencia en las líneas de visión, como las que van desde los ojos de un personaje hacia otro o hacia un horizonte o ciertas acciones dentro de la imagen como vuelos, caídas, trabajos, etc.).
- ¿Cómo describirías o caracterizarías el «movimiento interno» de la imagen, ya sea una pintura o un dibujo? En otras palabras, ¿qué te sugiere: texturas que se repiten, formas geométricas, remolinos, velocidad, ráfagas, caídas hacia adentro, sensación de desniveles, alturas, lentitud como de cámara lenta, estados de ánimo, fluidos, pegajosidad, clima, movimientos humanos o animales? (Hacer la «traducción» de un medio a otro, en este caso de lo visual y sensorial a lo verbal, siempre ayuda a liberar la imaginación).
- ¿Cómo se sugiere la profundidad en la imagen? (Esto ayuda a imaginar otras dimensiones en una imagen que es plana).
- ¿Cuál es la expresión facial o el lenguaje corporal de los personajes humanos, animales o fantásticos que aparecen en los dibujos y pinturas? (Esto permite desarrollar el «tejido social» o la lógica interna de las situaciones y de las relaciones que se dan dentro de la imagen: violencia, amor, tranquilidad, expectativa, dominancia, paridad, autoridad, sumisión, temor, alegría, etc.).
De los dibujos, pinturas, desarrollos y paradojas de Escher es posible aprender intuitivamente mucha matemática y dejarse hechizar por ella para luego emprender una búsqueda e investigación un poco más profunda.
Así surgirán términos como: orden, caos, simetría, asimetría, cóncavo, convexo, ascendente, descendente, infinito, finito, repetición, mosaicos, división del plano, rompecabezas o puzzle, circularidad, rotaciones, ángulos, series, patrones, fractales, estructuras, ciclos, perspectiva, ilusiones ópticas, multilinealidad, traslaciones, cristales, mundos simultáneos, superficie, espacio, laberintos, metamorfosis, bidimensionalidad, tridimensionalidad.
Cada uno de estos términos —y muchos otros más que descubrirán solos— despliega un abanico de posibilidades para continuar explorando.
¿Qué esperan para comenzar? ¡Adelante, escherianos!
Recomendados
Escher: el cruce maravilloso del arte con el hechizo de la matemática
Texto
Escher atravesó el alma de la matemática a través del arte para crear obras únicas. Dibujos, ensayos, desarrollos artísticos, pinturas, grabados... Toda la producción de este genial artista holandés señala —si estamos dispuestos a jugar, indagar y entregarnos a las paradojas— incitantes caminos de descubrimiento. ¿Y si ensayamos una nueva mirada y le tomamos el gusto a la otra matemática?
¿La matemática puede ser más romántica que una película de Hollywood?
Texto
La matemática es más que números y fórmulas; también es amor, seducción y misterio. A veces genera objetos fascinantes y paradojales como la cinta de Moebius. La topología puede parecer mágica; sin embargo, es una rama de la matemática. Los invitamos a dejarse hechizar con su ciencia.
Ficha
Publicado: 04 de febrero de 2019
Última modificación: 22 de abril de 2025
Audiencia
Docentes
Estudiantes
Familias
Área / disciplina
Matemática
Nivel
Primario
Secundario
Categoría
Artículos
Modalidad
Todas
Formato
Texto
Etiquetas
Matemática
arte
M. C. Escher
Autor/es
Carina Maguregui
Licencia
Creative Commons: Atribución – No Comercial – Compartir Igual (by-nc-sa)