La matemática incrustada en la inmensa variedad de formas de vida

¿Quién fue Fibonacci?

Leonardo de Pisa (1170 - 1240) también llamado Leonardo Pisano, Leonardo Bigollo o simplemente Fibonacci, fue un matemático italiano. Difundió en Europa la utilidad práctica del sistema de numeración indo-arábigo frente a la numeración romana y fue el primer europeo en describir la sucesión numérica que lleva su nombre. El apodo del padre de Leonardo, era Bonacci (simple o bien intencionado). Leonardo recibió póstumamente el apodo de Fibonacci (por filius Bonacci, hijo de Bonacci). El padre dirigía un puesto de comercio en el norte de África, de niño Leonardo viajó allí para ayudarlo y fue donde aprendió el sistema de numeración árabe.

Consciente de las ventajas de los numerales árabes (con un sistema de numeración decimal, notación posicional y un dígito de valor nulo: el cero), Fibonacci viajó a través de los países que rodeaban el mar Mediterráneo para estudiar con los matemáticos árabes más destacados de ese tiempo, regresando hacia el 1200.

En 1202, a los 32 años de edad, publicó lo que había aprendido en su libro Liber abaci («abaci» en el sentido de aritmética y no del ábaco como instrumento). Este texto mostró la importancia del nuevo sistema de numeración aplicándolo a la contabilidad comercial, conversión de pesos y medidas, cálculo, intereses, cambio de moneda, y otras numerosas aplicaciones. En estas páginas describe el cero, la notación posicional, la descomposición en factores primos y los criterios de divisibilidad. El libro fue recibido con entusiasmo entre el público culto, teniendo un impacto profundo en el pensamiento matemático europeo.

La sucesión de Fibonacci y la razón áurea

En matemática, la sucesión de Fibonacci se trata de una serie infinita de números naturales que empieza con un 0 y un 1 y continúa añadiendo números que son la suma de los dos anteriores:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…

La sucesión comienza con los números 0 y 1 y a partir de estos, «cada término es la suma de los dos anteriores», produciéndose una relación de recurrencia que la define.

El 1 se obtiene sumando  0 + 1= 1   /  el 2 se calcula sumando 1+1  /  análogamente, el 3 es 1+2  /   el 5 es 2+3    ¡Y sigue!

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...

¿Se animan a encontrar los números que le siguen al 317811?

Esta secuencia tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en la disposición de las ramas en los árboles, las hojas en los tallos, en las telas de arañas, en las hojas del alcaucil, en las flores de los girasoles y en las piñas de las coníferas, para nombrar algunos ejemplos comprobables a simple vista. La secuencia de Fibonacci se revela en diversas maneras a través de toda la naturaleza.

Y hay una sorpresa: si tomamos dos números de Fibonacci consecutivos (uno detrás del otro) y hacemos su división (cociente) el resultado es lo que se conoce como razón áurea "φ" (Phi) que tiene el valor aproximado 1.618034... De hecho, cuanto más grandes son los números de Fibonacci, aparecen más decimales en su cociente (tendiendo a infinito). 

Probemos con algunos:

 
Sintetizando: cuando se divide el número mayor de la serie de Fibonacci por el número inmediatamente menor en la serie, el resultado es 1,618. Si se divide el número menor por el mayor inmediatamente adyacente, la razón se aproxima a 0,618. Este cociente es conocido como razón o proporción áurea.

¿Por qué Fidias —el escultor griego— y otros en los antiguos países de Grecia y Egipto usaban a menudo esta razón en el diseño de muchas de sus obras de arte? Porque se había descubierto que esta razón era sumamente atractiva para el ojo humano; produce lo que se conoce como el rectángulo áureo. Si el lado corto del rectángulo es 1, el lado largo será 1,618. Esta forma rectangular se aproxima al patrón usado para el diseño del Partenón de Grecia, y para muchas de sus numerosas imágenes, de sus muchos vasos, portales, ventanas, estatuas e incluso para ciertos parámetros de la Gran Pirámide de Egipto. El edificio de las Naciones Unidas es un rectángulo áureo. Muchas de las cosas que usamos se diseñan de manera que se aproximan al rectángulo áureo: las tarjetas de crédito, los naipes, las placas de los interruptores, los blocs para escritura, etc.

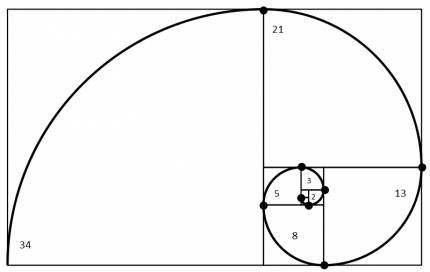
Una aproximación de la espiral áurea se genera dibujando arcos circulares conectando las esquinas opuestas de los cuadrados ajustados a los valores de la sucesión y adosando sucesivamente cuadrados de lado 0, 1, 1, 2, 3, 5, 8, 13, 21 y 34.

Artistas plásticos como Leonardo da Vinci, Van Gogh, Vermeer, Renoir y otros empleaban la proporción áurea, también llamada “dorada”, en muchos de sus trabajos. Tomaban «un lienzo en blanco y lo dividían entre áreas basándose en las proporciones áureas para determinar la situación de los horizontes, de los árboles, etc.».

Otra área de enorme interés es la aparición de la secuencia de Fibonacci en la disposición en espiral de las hojas alrededor de tallos de plantas (conocido como filotaxis). Este patrón en espiral se hace evidente al contemplar el tallo directamente desde encima, y observando el arco que el tallo forma desde la base de una hoja a la siguiente, y la fracción de la circunferencia del tallo que queda delineada. En cada caso, los números pertenecen a la sucesión de Fibonacci. Ejemplos: en el olmo el arco es 1/2 de la circunferencia; en el árbol de las avellanas, 1/3; en el roble, 2/5; en el peral y el álamo, 3/8; en el sauce, 5/13; y en algunos pinos: a veces 5/21 y otras 13/34. ¿Por qué esta disposición y no otra? Sucede que este patrón asegura que cada hoja recibirá la máxima exposición a la luz del sol y al aire, con el mínimo necesario de sombra y un bajo apiñamiento o amontonamiento respecto de otras hojas.

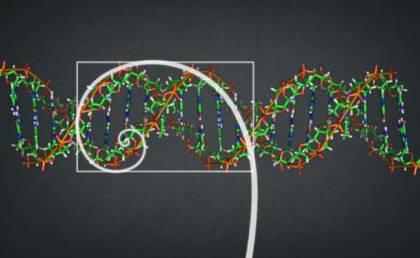
No debería sorprendernos, entonces, constatar que la molécula de ADN tiene una anchura de 21 Ǻngstroms y que la longitud de una vuelta entera en su espiral mide 34 Ǻngstroms, ambos números de Fibonacci. Además, la molécula de ADN es literalmente una larga secuencia de rectángulos áureos.

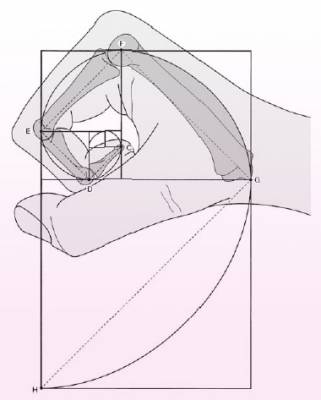
Las partes del cuerpo humano también están “organizadas” por los números de Fibonacci y la proporción áurea. Por ejemplo: en las manos cada sección de los dedos índice, desde la punta hasta la base de la muñeca, es más larga que la anterior, manteniendo el cociente de 1.618… y también adecuándose a los números Fibonacci: 2, 3, 5 y 8, si se van sumando de una en una cada sección de la mano. (En esta escala, la uña es la unidad de longitud.) En síntesis: tenemos 2 manos, cada una con 5 dígitos y 8 de nuestros dedos constan de 3 secciones. ¡Todos son números Fibonacci! 

Les proponemos ver el siguiente corto-documental sobre la proporción áurea

 

Los números, los conejos y la música

Mucho antes de ser conocida en occidente, la sucesión de Fibonacci ya estaba descrita en la matemática en la India. Pero fue Fibonacci quien la dio a conocer en Occidente como la solución a un problema de la cría de conejos: «Cierto hombre tenía una pareja de conejos en un lugar cerrado y deseaba saber cuántos se podrían reproducir en un año a partir de la pareja inicial, teniendo en cuenta que de forma natural paren una pareja de conejos en un mes, y que a partir del segundo mes se empiezan a reproducir». Así la reproducción de los conejos sigue la secuencia de Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13 ...

También Kepler describió los números de Fibonacci, y el matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números de Fibonacci sucesivos se acerca a la relación áurea Phi cuando “n” tiende a infinito. Esta sucesión tuvo popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores como Béla Bartók y Beethoven, entre otros, la utilizaron para la creación de acordes y de nuevas estructuras de frases musicales. 

Ahora bien en términos prácticos, si nos fijamos en el teclado de un piano, es muy fácil encontrar las proporciones áureas: hay 8 teclas blancas, 5 teclas negras y ellas aparecen en grupos de 2 y de 3. La serie 2 / 3 / 5 / 8 es, por supuesto, el comienzo de la serie de Fibonacci.

Si aun no se entiende, aclaramos que las notas de la escala son 8 (do, re, mi, fa, sol, la, si, do). Existen 5 alteraciones dadas por las teclas negras, y si sumamos ambos (8 + 5) da una totalidad de 13 notas en el piano (do, do#, re, re#, mi, fa, fa#, sol, sol#, la, la#, si, do).

Otro hecho curioso y para tener en cuenta es que: un acorde mayor está compuesto por las notas 1, 3 y 5 de una escala. El acorde mayor es un acorde lleno, completo, agradable y armonioso a diferencia de cualquier otro acorde compuesto con otros intervalos.

En 1915, Béla Bartók desarrolló un método para que todos los elementos -escalas, estructuras de acordes y proporciones de longitud- quedasen integrados según la razón áurea. Su planta favorita era el girasol, su estudio estaba lleno de piñas de coníferas y sostenía que la música popular también era un fenómeno natural al igual que las flores y los animales. 

Como cierre les dejamos la "Quinta Sinfonía" de Beethoven y una de las obras de Bartók: "Música para instrumentos de cuerda, percusión y celesta", en la que un análisis de musicólogos y matemáticos identificó la aparición de la sucesión de Fibonacci y de la razón áurea.