¿La matemática puede ser más romántica que una película de Hollywood?
La matemática es más que números y fórmulas; también es amor, seducción y misterio. A veces genera objetos fascinantes y paradojales como la cinta de Moebius. La topología puede parecer mágica; sin embargo, es una rama de la matemática. Los invitamos a dejarse hechizar con su ciencia.
¿El conocimiento matemático es tan importante al punto de convertirse en la clave de una resolución feliz para una historia de amor? ¿Tiene futuro una relación amorosa que comienza sobre una cinta de Moebius? La topología, además de ser la más joven de las ramas clásicas de las matemáticas, ¿es la más sentimental? ¿Son compatibles la matemática y las emociones?
Podríamos hacer unas cuantas preguntas más, pero estas parecen ser lo suficientemente interesantes como para empezar. En pleno siglo XXI, en el que se hacen estudios para prácticamente cualquier cosa, quedamos subyugados por la idea de qué difícil, importante y necesario es saber hacer buenas preguntas.
No nos interesa profundizar en fórmulas, ecuaciones ni abstracciones que nos provoquen dolores de cabeza, simplemente queremos hacer preguntas que generen desafíos diferentes y que intencionalmente no nos conduzcan a respuestas, sino a nuevos interrogantes derivados, cadenas de preguntas, redes y múltiples planteos con diversos itinerarios por recorrer.
¿Una historia de amor topológica?
Möbius strip (en inglés, 'Cinta de Moebius') es un cortometraje de animación de Link Pak Shing y Wan Ting Tifa, protagonizado por unos bellísimos personajes.
Luego de ver el corto, se nos agolpa una cascada de preguntas, preguntas que podemos ensayar aquí y responder en clase junto con los estudiantes:
- La cinta sobre la que están los personajes de la historia ¿dónde se encuentra?
- ¿Por qué decimos «cinta»? ¿Se trata realmente de una cinta?
- Por un momento, creamos fervientemente en el escenario del cortometraje y preguntémonos: si esta cinta permaneciera inalterada como en el inicio de la historia, ¿nuestros personajes se conocerían?
- ¿Podríamos decir que el primer corte de tijera lo hace Cupido? ¿Por qué pensamos en Cupido? ¿Qué produce el primer corte? ¿Qué tiene de importante?
- ¿Qué posibilidades se abren luego del primer corte de tijera y del empalme invertido de la cinta?
- Si bien el amor no tiene explicación —y eso lo hace tan misterioso y único—, ¿por qué uno de los personajes decide cruzar la línea punteada?
- ¿Cambia el escenario de la historia luego del segundo corte de tijera? ¿Los personajes han entendido qué sucedió? Y nosotros ¿qué pensamos que sucedió?
- En este punto, ¿cuánto puede hacer cada personaje por alterar el rumbo de la historia? ¿Alguno de los dos tiene ventaja sobre el otro? ¿Por qué?
- ¿Habría un final feliz para quienes saben matemática? ¿Habría un final triste para quienes no saben matemática?
- ¿Qué creen los personajes al final de la historia?
- Para nosotros, como espectadores, ¿la historia entre ellos terminó o podemos pensar que existe la posibilidad de un reencuentro? ¿Qué tendría que suceder, de ser posible, para que ese reencuentro ocurriera? ¿Esta posibilidad depende de los dos personajes o de uno de ellos?
- ¿Qué medida tiene el amor? ¿Tiene sentido esta pregunta?

Dibujo de Adam Pekalski
Más allá del ejercicio de formular todas las preguntas que podamos imaginar, es interesante indagar en los conceptos de topología y cinta de Moebius.
Topología: la geometría de la posición
La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece recién a finales del siglo XIX y principios del XX, con el nombre de analysis situs, es decir, 'análisis de la posición'.
De manera informal, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas.
El topólogo considera los mismos objetos que el geómetra, pero de modo distinto: no se fija en las distancias o los ángulos, ni siquiera en la alineación de los puntos. Para el topólogo, un círculo es equivalente a una elipse; una bola no se distingue de un cubo: se dice que la bola y el cubo son objetos «topológicamente equivalentes» porque se pasa de uno al otro mediante una transformación continua y reversible.
Algunos de los desafíos que estudia la topología
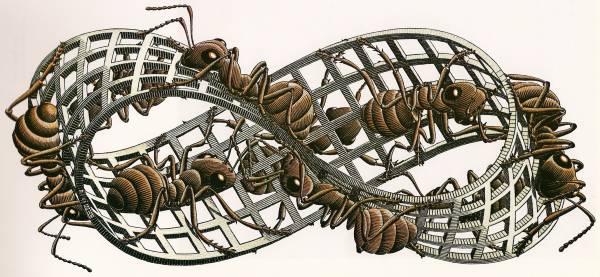
Cinta de Moebius dibujada por Escher
Tomen una cinta de papel y únanla por sus extremos para formar un anillo; eso sí, antes de pegarla giren uno de los extremos. La cinta resultante será la famosa cinta de Moebius: aunque no ha dejado de ser un objeto material y simple, posee una sola cara, cosa demostrable por el simple método de trazar sobre ella una línea, recorriendo toda la longitud del papel sin levantar el lápiz ni una sola vez: la línea concluirá donde empezó, mordiéndose la cola como la serpiente mitológica.
Si ahora uno apela a una tijera y corta la cinta siguiendo el trazo, no se obtendrán, como cualquiera esperaría, dos anillos de papel: será solamente uno. Otra rareza. Si se repite la operación, el resultado serán dos aros de cinta encadenados.
La cinta de Moebius es uno de los «juguetes» más amados de la topología. Inspiró los dibujos del holandés M. C. Escher y fue, entre otras cosas, el punto de partida para notables relatos fantásticos de Franz Kafka, Jorge Luis Borges y Adolfo Bioy Casares.
Moebius y el cine
La cinta también inspiró al norteamericano A. J. Deutsch a la hora de escribir «Un túnel llamado Moebius», relato publicado en 1950, cuando la topología hacía furor en el mundo de la ciencia ficción. La idea del cuento, magnífica por cierto, atrajo a Gustavo Mosquera R., uno de los pocos realizadores de cine en la Argentina que se animó a incursionar en el género.
Mosquera, docente de la Fundación Universidad del Cine, planificó un largometraje colectivo sobre el tema, es decir, gestado en su totalidad por un plantel de casi medio centenar de estudiantes, que se pusieron bajo su dirección general durante el año y medio que tardó en salir de los laboratorios. Según los espectadores que lo vieron y opinaron en el Festival de Cine de San Sebastián, en el film Moebius la metáfora es contundente: un vagón de tren con más de treinta pasajeros desaparece en el circuito cerrado de los subterráneos porteños. La tarea de búsqueda queda a cargo de un matemático especializado en topología, que no consigue dar con el viejo diseñador de la tranway hasta que, con la ayuda de una niña, logra entrar en carrera hacia la revelación final. El topólogo deduce que, a consecuencia de los múltiples cruces de vías, estas han creado una especie de cinta que interconecta con otra dimensión espacio-temporal.
Recomendados
La matemática incrustada en la inmensa variedad de formas de vida
Texto
Subyace una matemática sutil detrás de todo cuanto nos rodea, desde el patrón de crecimiento de un helecho hasta el trino de las aves, la disposición de los pétalos en las flores, la estructura del caparazón de ciertos moluscos y la espiral de una galaxia en el universo, por nombrar solo algunos entre cientos de ejemplos. La llamada sucesión de Fibonacci es una de las formas matemáticas para encontrar el denominador común entre los patrones y los diseños de la naturaleza.
¿Por qué no se caen los balcones? Al fin matemáticas sin fórmulas
Texto
El arquitecto y docente Mario Salvadori explicaba por qué los edificios permanecían de pie sin desplomarse. Lo más interesante es que lo hacía sin desplegar fórmulas terroríficas. La creatividad y la imaginación son las mejores aliadas de la matemática.
Escher: el cruce maravilloso del arte con el hechizo de la matemática
Texto
Escher atravesó el alma de la matemática a través del arte para crear obras únicas. Dibujos, ensayos, desarrollos artísticos, pinturas, grabados... Toda la producción de este genial artista holandés señala —si estamos dispuestos a jugar, indagar y entregarnos a las paradojas— incitantes caminos de descubrimiento. ¿Y si ensayamos una nueva mirada y le tomamos el gusto a la otra matemática?
Potencias de 10: ceros, átomos y el tamaño de todas las cosas
Texto
¿Cómo varía la cantidad o el tamaño al agregar o quitar un cero de una cifra? ¿Los átomos que componen a las hormigas y a los seres humanos pueden ser los mismos que constituyen a los planetas y a las galaxias, siendo que los tamaños y las complejidades son tan diferentes?
Las ilusiones ópticas de Escher impresas en 3D
Texto
No se trata de una ficción de Bradbury ni de Asimov; la impresión de objetos en tres dimensiones es un hecho. Más sorprendente aún es que una impresora 3D sea capaz de generar las estructuras imposibles del artista M.C. Escher.
Figuras, objetos y dimensiones: cómo despegar de Planilandia
Texto
¿Cómo pensamos los objetos que amamos? ¿Queremos explorar las formas en que las neurociencias y la cultura ven el mundo a través de las imágenes y de las ideas? ¿Nos atraen las novelas geométricas y las esferas parlantes...? Entonces estamos listos para dar el paso a la cuarta dimensión. Nos acompañarán en este fascinante recorrido dos libros y una película.
El número pi: la matemática de todas las cosas
Texto
El número pi es una constante matemática. Y en esta actividad los invitamos a conocer una película en la que el protagonista supone que pi es un número mágico que todo lo gobierna.
La belleza oculta de la matemática
Texto
Compartimos 13 recursos que abordan la matemática desde distintos ángulos, visiones y disciplinas. En las matemáticas, hay amor, prolifera el arte, emergen patrones, hipnotiza la naturaleza, circulan objetos increíbles y se generan paradojas, entre otras atracciones. Lo más importante es que les proponemos lecturas, videos y actividades ¡sin fórmulas y con mucha imaginación!
Ficha
Publicado: 04 de febrero de 2019
Última modificación: 21 de abril de 2025
Audiencia
Docentes
Estudiantes
Familias
Área / disciplina
Biología
Matemática
Ciencias Naturales
Nivel
Primario
Secundario
Categoría
Entrevistas, ponencia y exposición
Modalidad
Todas
Formato
Texto
Etiquetas
banda de Moebius
topología
enseñanza de la matemática
M. C. Escher
cine
Autor/es
Carina Maguregui
Licencia
Creative Commons: Atribución – No Comercial – Compartir Igual (by-nc-sa)


