Geometría bajo el agua: arrecifes de coral versus Euclides
La geometría hiperbólica revolucionó las matemáticas cuando fue descubierta en el siglo XIX, pero se pensaba que sus estructuras eran imposibles de recrear. Los corales tuvieron la respuesta en su propia morfología durante aproximadamente 50 millones de años, pero no fue hasta 1997 que Daina Taimina -una matemática de la Universidad de Cornell, EE.UU- comprendió que ese tipo de estructuras ¡se podían tejer! En 2005, dos hermanas, Margaret y Christine Wertheim: una científica y una artista iniciaron un proyecto que consiste en tejer corales al crochet. Esos tejidos son estructuras hiperbólicas.
Aprendiendo geometría de la mano de los corales y el crochet
Margaret Wertheim es una científica y escritora australiana que junto a su hermana artista fundó un proyecto del que ahora participan miles de personas en tres continentes. Las raíces del emprendimiento abarcan los campos de las matemáticas, la biología marina, las artesanías femeninas y el activismo ambiental. El desarrollo de este proyecto se equipara con la evolución de la vida en la Tierra y consiste en tejer arrecifes de coral.
Las mellizas Margaret y Christine comenzaron el proyecto de tejer corales al crochet en 2005. Durante ese año se hablaba mucho del calentamiento global y de su incidencia en los arrecifes de coral. Los corales son organismos delicados y muy sensibles a cualquier incremento en la temperatura del mar. Pequeñas variaciones de la temperatura provocan decoloraciones que son los primeros signos de enfermedad en los corales. Si el aumento persiste, si las temperaturas no bajan, los arrecifes empiezan a morir. Este fenómeno viene sucediendo en la Gran Barrera de Coral y en los arrecifes de coral de todo el mundo desde hace décadas.

¿Por qué tejer un arrecife de coral?
La lana y la humedad no son precisamente dos conceptos que vayan bien juntos. ¿Por qué no cincelar un arrecife de coral en mármol o fundirlo en bronce? Hay una muy buena razón para tejerlo y es que la mayoría de los organismos del arrecife de coral tiene un tipo de estructura muy particular. La forma irregular que uno ve en corales, algas marinas y esponjas es una forma de geometría conocida como geometría hiperbólica. Y la única manera que conocen los matemáticos de modelar esta estructura es con el tejido crochet, ni siquiera pueden hacerlo con computadoras. Entonces, ¿de qué se trata la geometría hiperbólica que encarnan los corales y las babosas de mar?
Esta clase de geometría revolucionó las matemáticas al ser descubierta en el siglo XIX pero no fue hasta fines del siglo XX que los matemáticos comprendieron la manera de modelarla. En 1997, Daina Taimina, una matemática de la Universidad de Cornell, descubrió que esta estructura podría representarse en tejido crochet. Lo que en realidad estaba haciendo era un modelo de una estructura matemática que muchos estudiosos habían pensado que era imposible. Algunos de los mejores matemáticos de la historia pasaron cientos de años intentando demostrar que esta estructura no podía representarse porque desafiaba los teoremas descubiertos por Euclides 2.000 años atrás.
Las estructuras resultantes del tejido crochet representan tridimensionalmente el concepto de geometría hiperbólica, que de hecho existe en la naturaleza en criaturas como los corales.
Wertheim y colaboradores comenzaron a experimentar con el tejido y descubrieron que si se desviaban de las reglas específicas del código matemático que subyace al algoritmo simple: `tejer tres, incrementar uno´ y adornaban el código, los modelos inmediatamente comenzaban a verse más naturales. Los colaboradores de todo el mundo hicieron sus propias ornamentaciones, tejiendo corales únicos e irrepetibles. Así como la morfología y la complejidad de la vida terrestre no tienen fin, y hoy sabemos que diversas mutaciones y complejizaciones del código en el ADN producen nuevos seres como jirafas u orquídeas, del mismo modo las pequeñas ornamentaciones en el código crochet dieron paso a nuevas y extraordinarias criaturas en el árbol evolutivo de la vida al crochet.

De Euclides y su espacio plano hacia la geometría hiperbólica
Antes de la geometría hiperbólica, sabíamos de dos tipos de espacio: el euclidiano y el esférico.
El primero es el más familiar, el que aprendimos en la escuela, ese que nos pregunta cuántas líneas rectas pueden pasar por un punto fuera de una línea recta sin cruzarse con ella.

La respuesta es una: la paralela.

Pero si la línea y el punto están en una esfera, ¿cuántas pueden pasar?
Sobre la superficie de una esfera una línea recta es el círculo más grande posible que uno pueda trazar, ejemplo: la línea del Ecuador. Entonces la respuesta es: ninguna, pues eventualmente todas se unen, como ocurre con las líneas que cruzan los hemisferios en el globo terráqueo y se unen en los polos.
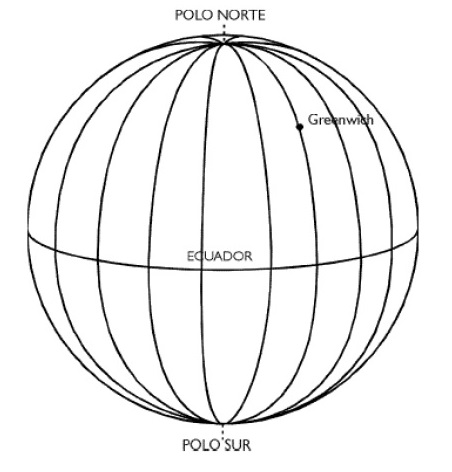
Hasta ahí, los espacios euclidiano y esférico son comprensibles... pero si sos matemático y tenés una pregunta cuyas respuestas son 1 y 0, hay una tercera opción que se hace evidente: infinito.
Entonces, si por ese punto deben pasar un infinito de líneas rectas que nunca se crucen con la línea original, habría que representarlo así:
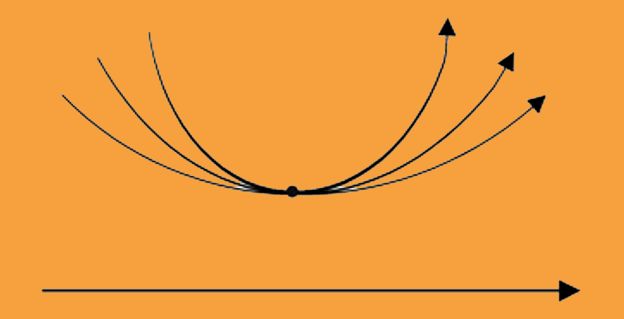
Esto fue lo que enloqueció a los matemáticos por tanto tiempo. Las líneas se ven curvas, no rectas. Pero eso es porque lo estaban representando en una superficie plana. Lo que Daina Taimina demostró fue que, así como para entender la respuesta en el caso del punto en la esfera nos valimos del globo terráqueo, el espacio hiperbólico también requería de otra superficie. Las formas rizadas que se tejen con una aguja de crochet y lana crean la superficie indicada. Recordemos que queremos comprobar que es posible que un infinito número de líneas rectas pasen por un punto sin cruzarse con la línea recta original.
En este tejido hecho por Margaret, en la parte superior está la línea original recta. Las demás pasan por un punto pero no se cruzan con la original.

Aunque estas últimas no parecen rectas, lo son, y no hay más que doblar el tejido a lo largo de cualquiera de esas líneas para demostrarlo. Así que aquí, en lana, con un arte casero femenino, está la prueba de que el postulado más famoso de las matemáticas está equivocado.

Los números del arrecife tejido
- 915 m² de superficie
- 3 metros de altura (las piezas más altas de coral alcanzan los 3 metros)
- 2,5 a 5 cms es el tamaño de las piezas más pequeñas y a menudo las más complejas
- 100 horas de trabajo toma hacer cada una de las diminutas torres de coral en crochet
Hay más de 40 arrecifes satélite en el que participaron:
- 10.000 personas de 3 continentes
- 1.000 pares de manos tejieron el arrecife satélite más grande del mundo que está en el Instituto Smithsonian en Washington.
- 700 mujeres de Alemania y Dinamarca tejieron el arrecife del Museo Kunst der Westkuste de Alemania

En una entrevista para la BBC, Margaret explicó:
«Cuando hacemos los talleres con este proyecto yo dedico la primera media hora a hablar de matemáticas y las diferentes formas y geometrías. Les explico también que el descubrimiento de la geometría hiperbólica fue muy importante en la historia de las matemáticas pues le mostró a los matemáticos que otros tipos de geometrías eran posibles. Fue una revolución que llevó a una geometría no euclidiana y las matemáticas de esa geometría fueron las que usó Albert Einstein en su teoría de la relatividad. Lo más interesante de tejer formas hiperbólicas es que se aprenden fundamentos de matemáticas y física con las manos, es poner a pensar al cuerpo».

Las hermanas Wertheim fundaron entonces el Institute For Figuring (IFF) convencidas de que ideas que -por lo general- se presentan en términos abstractos a menudo pueden ser traducidas en actividades físicas tan atractivas que terminemos comprendiéndolas como si estuviéramos jugando en un jardín de infantes. Margaret denomina a esta forma de hacer / aprender cosas: la usina de juego (play tank). La usina de juego, como la de pensamiento, es un lugar donde la gente puede ir y entrar en contacto con las grandes ideas. Todo el conocimiento, aún en los más altos niveles de abstracción como son las matemáticas, la computación, la lógica, etc., todo puede ser incorporado no sólo a través de métodos simbólicos algebraicos meramente cerebrales, sino, literalmente, jugando físicamente con las ideas.
Cerrando su charla en TED Werthein concluía:
«Incluso los matemáticos, que en un sentido son los más libres pensadores, no pudieron ver no sólo las formas de los corales a su alrededor sino la lechuga en sus platos. Porque la lechuga, y todos los vegetales enroscados, son encarnaciones de la geometría hiperbólica. En cierto modo, los matemáticos tenían una visión tan simbólica y acotada de la geometría que no fueron capaces de ver lo que sucedía con la lechuga que tenían frente a sus ojos. La naturaleza está llena de maravillas hiperbólicas».

Créditos de las fotografías corales de crochet: IFF-Crochet Coral Reef Gallery
Fuentes de este recurso: IFF, TED y BBC
Ver la charla completa de Margaret Wertheim en TED (subtitulada en español)
Ver la charla de Daina Taimina (subtitulada en español)
La vida de los corales (subtitulado en español)
Recomendados
La matemática incrustada en la inmensa variedad de formas de vida
Texto
Subyace una matemática sutil detrás de todo cuanto nos rodea, desde el patrón de crecimiento de un helecho hasta el trino de las aves, la disposición de los pétalos en las flores, la estructura del caparazón de ciertos moluscos y la espiral de una galaxia en el universo, por nombrar solo algunos entre cientos de ejemplos. La llamada sucesión de Fibonacci es una de las formas matemáticas para encontrar el denominador común entre los patrones y los diseños de la naturaleza.
La ecuación matemática escondida en las pinturas de Vincent van Gogh
Texto
Uno de los aspectos más extraordinarios del cerebro humano es su habilidad para reconocer patrones y describirlos. Entre los patrones más complicados de entender está el concepto de turbulencia en la dinámica de fluídos. Con su pintura “La noche estrellada” (1889), Vincent van Gogh se adelantó casi sesenta años al matemático Kolmogorov en el entendimiento intuitivo del fenómeno de la turbulencia. En este recurso les mostramos cómo el arte puede hacer ciencia.
La belleza oculta de la matemática
Texto
Compartimos 13 recursos que abordan la matemática desde distintos ángulos, visiones y disciplinas. En las matemáticas, hay amor, prolifera el arte, emergen patrones, hipnotiza la naturaleza, circulan objetos increíbles y se generan paradojas, entre otras atracciones. Lo más importante es que les proponemos lecturas, videos y actividades ¡sin fórmulas y con mucha imaginación!
Ficha
Publicado: 04 de febrero de 2019
Última modificación: 16 de abril de 2025
Audiencia
Docentes
Estudiantes
Familias
Área / disciplina
Ciencias Sociales
Matemática
Ciencias Naturales
Nivel
Secundario
Categoría
Actividades
Modalidad
Todas
Formato
Texto
Etiquetas
matemáticas
Euclides
geometría
coral
naturaleza
Autor/es
Carina Maguregui
Licencia
Creative Commons: Atribución – No Comercial – Compartir Igual (by-nc-sa)

