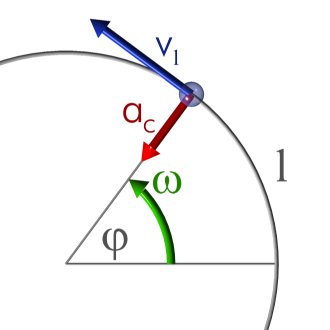
Movimiento circular uniforme. Modelado numérico
 |
Autor: Hernán Ferrari Responsable
disciplinar: Silvia Blaustein Área
disciplinar: Física Temática:
Movimiento circular. Movimiento en dos dimensiones. Fuerza
centrípeta Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar |
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En
ausencia de fuerzas netas, un cuerpo se mantendrá en movimiento
rectilíneo uniforme (MRU). Su velocidad (recuerden que se trata de un
vector) se mantendrá constante, que es la característica del MRU. Por
el contrario, si la velocidad no se mantiene constante,
dará como resultado una aceleración: 
,
y en consecuencia deberá existir una fuerza neta diferente de cero. El
cambio en la velocidad puede producirse por un cambio en su módulo, y
a
la aceleración asociada se la denomina aceleración tangencial (
)
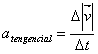por ser tangente a la trayectoria y paralela al desplazamiento y al
vector velocidad. Por otra parte, el cambio en la velocidad puede
deberse a una variación en la dirección del vector velocidad. A esta
aceleración se la llama aceleración centrípeta o normal, por ser
perpendicular a la trayectoria y al desplazamiento. Al producirse una
variación en la dirección de la velocidad, que es proporcional al
desplazamiento, la trayectoria de la partícula no será rectilínea. Por
lo tanto, en toda trayectoria que no sea rectilínea, existirá una
aceleración centrípeta.
El
módulo de la aceleración centrípeta es igual al cuadrado del módulo de
la velocidad dividido por el radio de curvatura de la trayectoria (cuán
curvada es la trayectoria):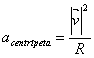 
.
Por último, si el cambio en la velocidad ocurre tanto en su módulo
como
en su dirección, entonces aparecerán las dos aceleraciones
mencionadas.
Objetivo de las actividades
Que los alumnos analicen el movimiento circular uniforme y resuelvan numéricamente problemas en dos dimensiones.
Actividad 1: Movimiento circular uniforme
En el movimiento circular uniforme, un cuerpo se mueve en una trayectoria circular manteniendo el módulo de su velocidad constante. De esta forma, la aceleración tangencial es nula y solo existe una aceleración centrípeta y, por lo tanto, una fuerza centrípeta que, como es perpendicular a la trayectoria, apunta siempre en dirección al centro de la circunferencia.
Se tomará entonces un sistema de referencia centrado en la circunferencia. Como el módulo de la velocidad es constante, el módulo de la aceleración centrípeta también lo va a ser, ya que es igual al módulo de la velocidad al cuadrado dividido el radio de curvatura, que también es constante e igual al radio de la circunferencia. Por otro lado, la aceleración será paralela a la posición del cuerpo, como se puede ver en la siguiente figura:
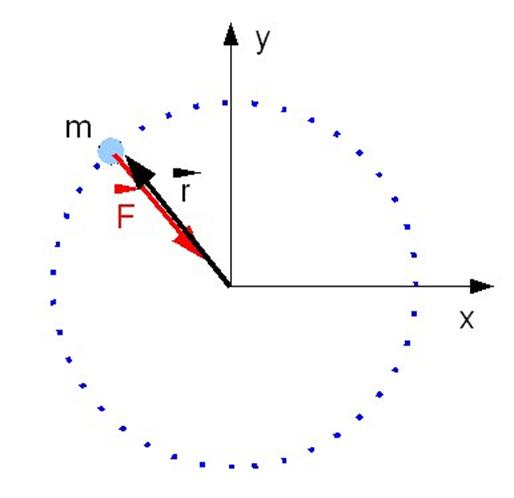
Este es entonces un problema en dos dimensiones, que se resolverá como se hace en el caso de una dimensión, para cada componente de los vectores. Así, los vectores posición, velocidad, aceleración y fuerza serán:
Como en el caso unidimensional, se resolverá utilizando:
En forma análoga, se podrán calcular los cambios en las componentes de la velocidad:
Solo resta poder sacar las componentes de la aceleración. Se sabe que estará en la dirección del vector posición y tendrá sentido contrario. Además, que su módulo será constante e igual al cuadrado del módulo de la velocidad, dividido por el radio de la circunferencia. Luego, para tener la dirección del vector aceleración, se usará el vector posición, dividido por el módulo de este vector. Entonces el vector aceleración será:
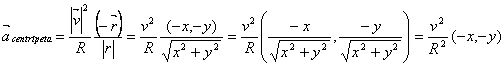
Fíjense que lo que se acaba de encontrar en el paréntesis del anteúltimo término no es otra cosa que el coseno y el seno del ángulo que forma el vector posición, como se suele hacer para descomponer vectores al utilizar trigonometría.
Resuelvan el siguiente problema numéricamente:
a. Encuentren la posición en función del tiempo para un movimiento circular uniforme con condiciones iniciales: posición inicial (0,3 m) y velocidad inicial (-2 m/s, 0).
- Grafiquen la coordenada x y la coordenada y en función del tiempo.
- Grafiquen la coordenada y en función de la coordenada x.
- Verifiquen con los resultados calculados que el módulo del vector velocidad sea constante.
- Calculen el ángulo del vector posición en función del tiempo y grafíquenlo.
- En el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos de esta actividad. Incluyan los programas y los gráficos realizados.
Movimiento circular uniforme Actividad 1
Actividad 2: Problema de encuentro en el movimiento circular uniforme
a. Piensen en el movimiento circular uniforme que realizan las agujas de un reloj analógico. ¿A qué hora la aguja de las horas y la de los minutos se encuentran en una misma posición angular? Hallen las diez posiciones de encuentro distintas a la trivial, que corresponde a la hora doce.
b. En el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos de esta actividad. Incluyan los programas y los gráficos realizados.
Movimiento circular uniforme Actividad 2