Tiro vertical 2. Modellus
 |
Autor: Hernán Ferrari Responsable
disciplinar: Silvia Blaustein Área
disciplinar: Física Temática:
Movimiento rectilíneo uniformemente variado. Software Modellus
Nivel: Secundario, ciclo básico Secuencia
didáctica elaborada por Educ.ar |
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se continuará con la resolución numérica de problemas de física y se resolverá un problema de tiro vertical utilizando el software Modellus. Se analizarán las diferencias que presenta este programa con el software Scilab.
Objetivo de las actividades
Que los alumnos resuelvan y visualicen un problema de tiro vertical utilizando el software Modellus, resaltando sus ventajas y desventajas frente al software Scilab.
Actividad 1
En esta secuencia resolverán un problema utilizando el Modellus, que permitirá ver el movimiento del cuerpo. Podrán comprender cómo realizar la visualización con la solución conocida para el MRUV, y también cómo resolver el problema con el modelado numérico tal como se hizo en otras secuencias con el programa Scilab.
Podrán observar que existen diferencias en la resolución realizada por ambos programas. Por un lado, el Scilab es mucho más veloz que el Modellus, pero este último programa es mucho más atractivo visualmente, ya que muestra en simultáneo el gráfico, la tabla de valores y el movimiento del cuerpo.
1.
Resuelvan
entonces el siguiente problema utilizando el Modellus: un
jugador de béisbol profesional puede arrojar una pelota de béisbol en
dirección vertical con una velocidad inicial de ![]() m/s.
m/s.
a) Utilicen las ecuaciones para el movimiento rectilíneo uniformemente variado. Para ello, en la ventana de «modelo matemático» del Modellus escriban las ecuaciones del MRUV para las variables x1 y v1, en las que se hn tomado un sistema de referencia con origen en la posición inicial de la pelota positivo hacia arriba y para un valor de la aceleración de la gravedad de 10 m/s2.
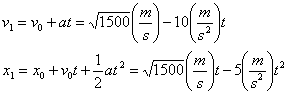

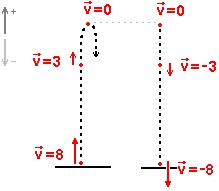
b) Como en la secuencia de MRU (ver secuencia MRU), agreguen en el fondo blanco del espacio de trabajo una partícula a la que se le asignará la variable x1 en la coordenada vertical. También se cambiará la escala vertical a 4 píxeles por cada unidad. En la variable independiente se dará un paso de 0.1 entre un valor mínimo de 0 y máximo de 8.
Por último, agreguen un nuevo objeto en el espacio de trabajo: un vector. Para ello, con el botón derecho seleccionen «crear vector» y a este objeto asígnenle 0 en la coordenada horizontal; en la vertical den el valor de la velocidad v1 y, por último, más a la derecha, seleccionen «unir objeto a» y «Partícula 1». De esta forma podrán ver el objeto subiendo y, junto con su movimiento en cada paso, cómo va variando el vector velocidad.
c) Aprieten el botón verde de abajo a la izquierda y podrán visualizar la solución del problema. ¿En qué tiempo y cuánto vale la altura máxima? Comparen este resultado con el que obtuvieron analíticamente. La solución debe resultar similar a la que pueden observar en el siguiente video MRUV1.
Nota: este video fue realizado capturando la pantalla en Linux con el programa XVidCap y en él se observa que el resultado del Modellus coincide con el resultado analítico.
d) En el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Mediante capturas de pantalla, incluyan los programas utilizados y los gráficos que hicieron.
Actividad 2
1. En esta actividad resolverán el
problema de la actividad 1
utilizando el modelado numérico similar al Scilab, pero ahora con el
lenguaje del Modellus: un jugador de béisbol profesional puede arrojar
una pelota de béisbol en dirección vertical con una velocidad inicial
de ![]() m/s.
m/s.
a) Para la resolución, agregarán al «modelo matemático» las variables x2 y v2 como lo harían en el Scilab, usando solo relaciones lineales y actualizando la aceleración y la velocidad en cada paso. En este caso, la aceleración es constante, por lo que las ecuaciones para el primer paso para la velocidad y la posición resultan:
![]()
y en general en el paso i+1 son:
![]()
Esto se puede escribir en el modelo matemático con la función que trae este software para considerar el último valor que tomó una variable con el comando Last. Con el modelado numérico, el modelo matemático resulta:
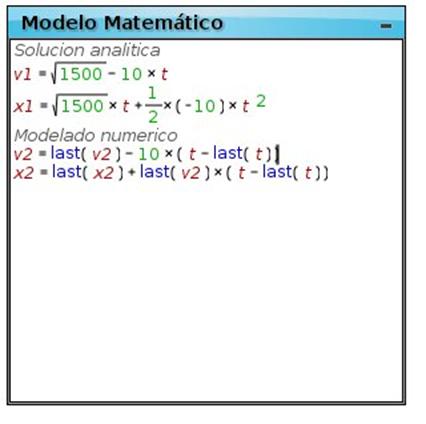
b) Agreguen otra partícula en el espacio de trabajo, a la que le asignarán la variable x2 en la coordenada vertical. También cambiarán la escala vertical a 4 píxeles por cada unidad. En la variable independiente darán un paso de 0.1 entre un valor mínimo de 0 y máximo de 8, como en la actividad anterior. También agregarán un vector para ver la velocidad.
c) Tanto la visualización de la solución analítica y como la del modelado numérico pueden verse en el siguiente video: MRUV modelado numérico con Modellus.
Nota: en el video se muestran las dos partículas: a la izquierda, la que corresponde a la solución analítica; a la derecha, la del modelado numérico. En el gráfico, la primera está con línea azul, mientras que la segunda, con línea roja.
d)
Disminuyan el paso del tiempo a 0.01 para ver cómo mejora la solución
del modelado numérico. Aquí es donde se ven las diferencias con las
escuencias donde se utilizó el programa Scilba. la
resolución del problema utilizando el Scilab.
e) En el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Incluyan los programas utilizados y los gráficos que hicieron.