Fuerzas: modelado numérico
 |
Autor: Hernán Ferrari Responsable
disciplinar: Silvia Blaustein Área
disciplinar: Física Temática: Fuerzas
sobre partículas. Dinámica Nivel:
Secundario, ciclo básico Secuencia didáctica
elaborada por Educ.ar |
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
El objetivo de la dinámica es el estudio de las fuerzas que actúan sobre un cuerpo para luego, con la relación a través de la masa (inercia del cuerpo), relacionar la resultante de todas las fuerzas con la aceleración. Una vez obtenida la aceleración puede calcularse la velocidad y luego con esta última, la posición. A continuación, verán cómo resolver estos problemas con la ayuda de una computadora a través del modelado numérico. Esta forma de trabajo permitirá resolver innumerables problemas sin necesidad de hacerlo analíticamente.
Objetivo de las actividades
Que los alumnos desarrollen el modelado numérico aplicado a la dinámica de partículas para determinar su movimiento utilizado para un caso unidimensional.
Actividad 1: Fuerzas y dinámica
El concepto fundamental que está detrás de este tipo de
soluciones es el siguiente: si
se la ve desde muy cerca, cualquier función se va a parecer una
recta.
Esta
aproximación de una función por un comportamiento lineal (recta), se
puede realizar dividiendo el intervalo sobre el que se quiere hallar
la
solución del problema en un número grande de intervalos pequeños. En
cada intervalo se va a suponer que la velocidad varía linealmente,
esto
es, tomar la aceleración constante en ese intervalo pequeño de tiempo,
lo que dará un cambio lineal para la velocidad. Aplicando el mismo
principio para la posición, se supone la velocidad constante durante
el
pequeño intervalo de tiempo, para así calcular el cambio en la
posición.
Para comenzar, se observarán los conocimientos de cinemática y las definiciones de posición, velocidad y aceleración.
La definición vista para la velocidad media está dada por:
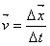
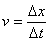
o vectorialmente
Por ahora se continuará con el planteo para el caso rectilíneo (en una sola dimensión) y más adelante se retomará la problemática vectorial.
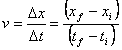
Despejando de esa definición de velocidad media, se puede obtener:
![]()
Conociendo la posición
inicial ![]() ,
la velocidad media
,
la velocidad media ![]() y
el pequeño intervalo de tiempo,
esta relación permite calcular la
y
el pequeño intervalo de tiempo,
esta relación permite calcular la
![]()
velocidad que tendrá luego de ese intervalo de tiempo, lo que se
denomina la posición final ![]() .
.
Considerando esta posición final como la posición inicial para el siguiente pequeño intervalo, se puede calcular cómo varía la posición en el siguiente intervalo de tiempo. Sin embargo, habrá que ver cuánto vale la velocidad en este nuevo intervalo. Para ello, se trabaja de forma análoga a lo realizado con la velocidad y la posición, pero esta vez con la aceleración y la velocidad.
La definición para la aceleración media está dada por:
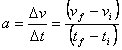
Despejando de esa definición de aceleración media, se puede obtener:
![]()
Igual que antes,
conociendo la velocidad inicial ![]() ,
la aceleración media
,
la aceleración media ![]() y
el
pequeño intervalo de tiempo,
esta relación
y
el
pequeño intervalo de tiempo,
esta relación
![]()
permite calcular la velocidad que tendrá luego de
ese intervalo de tiempo, lo que se denomina la velocidad final ![]() .
.
Finalmente, entran en juego la fuerza y la dinámica. La última dirá cómo cambia la fuerza a lo largo de los distintos intervalos de tiempo, y así permitirá utilizar la correspondiente aceleración, como la fuerza sobre la masa, en cada pequeño intervalo.
1. Resuelvan un problema sencillo con aceleración constante: se deja caer una piedra, que parte del reposo, desde lo alto de un edificio, a una altura de 75 metros. ¿Con qué velocidad llega al piso y cuánto tarda en llegar?
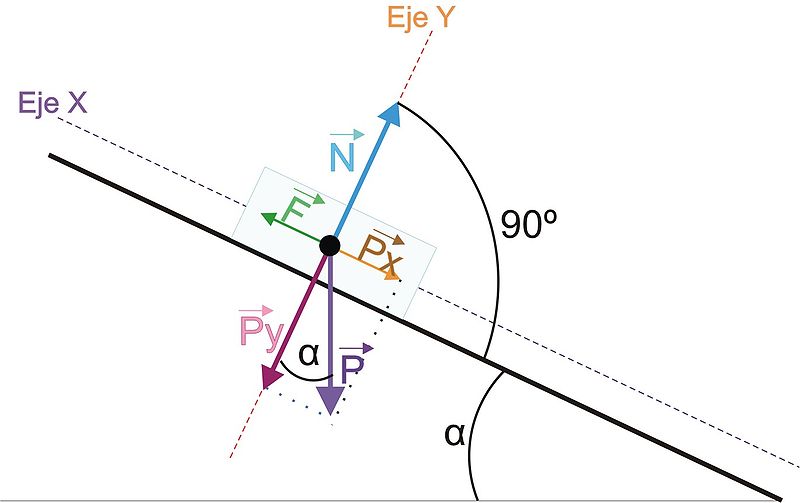
a) Realicen un diagrama de cuerpo libre para ver que la resultante de las fuerzas sobre el cuerpo es igual a la fuerza peso.
b) Planteen un sistema de coordenadas con el eje y en la dirección vertical, con origen en el piso, y la dirección positiva del eje hacia arriba.
c) Resuelvan primero analíticamente. Consideren la aceleración de la gravedad en la superficie de la Tierra igual a 10 m/s2.
d) Realicen un gráfico de la posición, la velocidad y la aceleración en función del tiempo.
Actividad 2: Resolución numérica
Planteando las condiciones iniciales según el sistema de
referencia mencionado, la aceleración será ![]() = -10 m/s2, la
velocidad inicial
= -10 m/s2, la
velocidad inicial ![]() =
0 m/s y la posición inicial
=
0 m/s y la posición inicial ![]() =
75 m.
=
75 m.
Trabajando con el Scilab, se pueden realizar los pasos repetitivos de manera sencilla y rápida. Para ello se trabajará con vectores, donde se colocarán en posiciones sucesivas de los vectores los valores correspondientes a intervalos de tiempos sucesivos. Se obtendrán así los vectores tiempo, posición, velocidad y aceleración. Se comenzará colocando los valores iniciales a cada vector:
Aceleración (1) = -10;
Velocidad (1) = 0;
Posición (1) = 75;
Tiempo (1) = 0.
De la resolución analítica, se puede estimar que el tiempo en llegar al suelo será menor a 4 segundos, por lo que ese será el intervalo de tiempo que se estudiará.
Se comenzará dividiendo el intervalo para estudiar en 10 intervalos iguales, por lo que los pequeños intervalos serán de 4 s/ 10. Para ello se hará un ciclo con 10 iteraciones, en el que en cada paso se calcularán los valores de posición, velocidad y aceleración de cada intervalo, ubicándolos en la posición de los vectores que les corresponda. Así continuará el programa:
for i = 1:10
tiempo (i + 1) = tiempo (i) + (4/10);
aceleración (i + 1) = -10;
velocidad (i + 1) = velocidad (i) + aceleración (i) * (tiempo (i + 1) – tiempo (i));
posición (i + 1) = posición (i) + velocidad (i) * (tiempo (i + 1) – tiempo (i));
end
1. Realicen un gráfico de la posición, la velocidad y la aceleración en función del tiempo, y compárenlos con las soluciones analíticas.
2. Modifiquen el programa para que divida el intervalo de tiempo de 4 segundos en 100, 1.000 y 10.000 intervalos iguales. Indiquen en un mismo gráfico cómo cambian las soluciones del problema al ir tomando intervalos más pequeños. Si al achicar el intervalo no se ven cambios en la solución, se considera que se ha llegado a la solución correcta.
3. Utilizando un ciclo y una condición, recorran los valores de la posición en función del tiempo en el caso de 1.000 intervalos, hasta encontrar el primer valor de posición negativa, que corresponderá aproximadamente al momento en que la piedra choca con el piso (posición = 0 m). Comparen este valor con el obtenido en la solución analítica.
Más adelante se verá un algoritmo para encontrar un momento más cercano al verdadero valor del tiempo en el que choca con el piso (método para hallar el cero o la raíz de una ecuación en la Actividad Tiro vertical y caída libre. Modelado numérico).
4. En el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Incluyan los programas y los gráficos realizados.