Movimiento rectilíneo uniforme (MRU)

	Autor: Hernán Ferrari Responsable disciplinar: Silvia Blaustein Área disciplinar: Física Temática: Movimiento en una dirección con velocidad constante Nivel: Secundario, ciclo básico Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

El movimiento rectilíneo uniforme es el movimiento más simple para estudiar. En él, un cuerpo se mueve sobre una recta, por lo que para describir su posición alcanza con utilizar la coordenada sobre un solo eje que coincida con la recta del movimiento. Por otro lado, la velocidad con la que se mueve el cuerpo es constante, por lo que la aceleración será cero.

Se aprovechará este tema para introducir el software Modellus, ya instalado en los equipos portátiles, que les permitirá visualizar muy fácilmente los problemas de Física una vez que tengan la solución matemática que modeliza el problema físico real.

Objetivos de las actividades

Que los alumnos:

1. Resuelvan problemas para movimientos rectilíneos uniformes.
2. Aprendan el manejo de ciertos comandos básicos del software Modellus.

Actividad 1: Movimiento rectilíneo uniforme con Modellus

El Modellus es un excelente programa escrito en lenguaje JAVA, que les permitirá visualizar las soluciones que brinda el modelado matemático para distintos problemas de la Física. Comenzarán estudiando los pasos para seguir, a fin de observar un movimiento rectilíneo uniforme.

1. Supongan el problema de un cuerpo que se mueve con MRU a una velocidad constante de 20 m/s.

a) Consideren un sistema de referencia cuyo eje x coincida con la recta en la que se mueve el cuerpo, y cuyo eje positivo coincida con la dirección en la que se desplaza el cuerpo. Tomen el origen del sistema de referencia con la posición del cuerpo al tiempo inicial, que también tomarán como cero.

b) Resuelvan el movimiento de forma analítica. ¿Qué tiempo le lleva recorrer 130 metros?

Para visualizar el problema en el programa Modellus, ábranlo desde el menú de programas de sus equipos portátiles. Se abrirá una ventana como la siguiente:

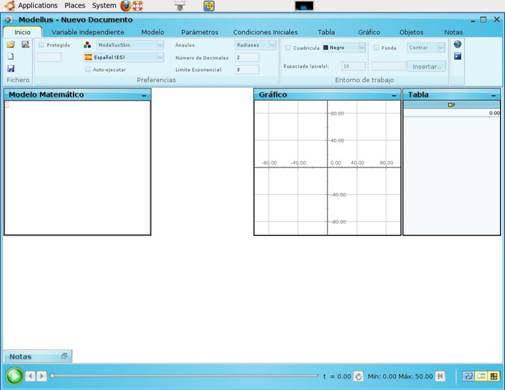
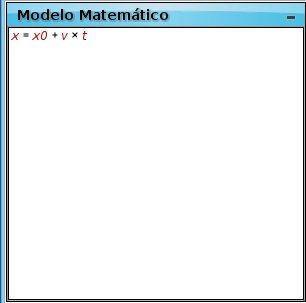
En la ventana de la izquierda («Modelo Matemático») escriban las ecuaciones que describen el movimiento según cada caso. En esta oportunidad, las ecuaciones son las de un MRU por lo que escribirán:

En la ventana deberán poner explícitamente los símbolos matemáticos para que la computadora los pueda comprender, por lo que hay que escribir el * para separar la velocidad del tiempo.

Lo que hace el programa Modellus son ciclos donde se calculan los distintos valores, en este caso, de la variable dependiente x. Para ello tiene que tener una variable independiente (generalmente el tiempo, t) y luego las condiciones iniciales que, para este caso, son .

Agreguen en el espacio de trabajo, en el fondo de la ventana principal, un objeto que será el que represente el cuerpo del que quieren ver su movimiento. Para ello, en la ventana principal, toquen el botón derecho y aparecerá un menú en el que deberán elegir la primera opción («Crear partícula»).

Luego, como se ve en la siguiente imagen, en la parte superior de los menús, aparecerán las coordenadas de la partícula a la cual le asignarán, en «Horizontal», la variable x, y, en «Escala», pondrán «3 píxeles igual a una unidad» para ver mejor el problema.

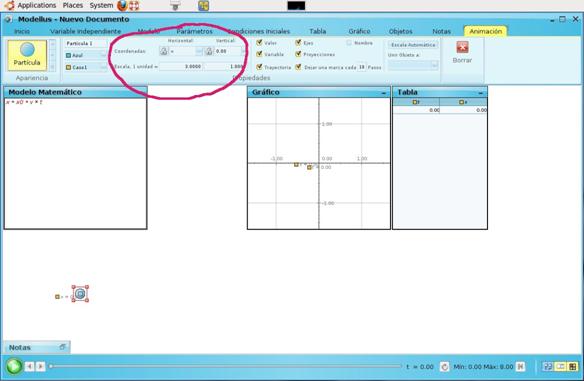
Solo falta dar los valores para las condiciones iniciales. En el menú de parámetros, pueden colocar los valores para x₀ y v, correspondientes a 0 m y 20 m/s, respectivamente.

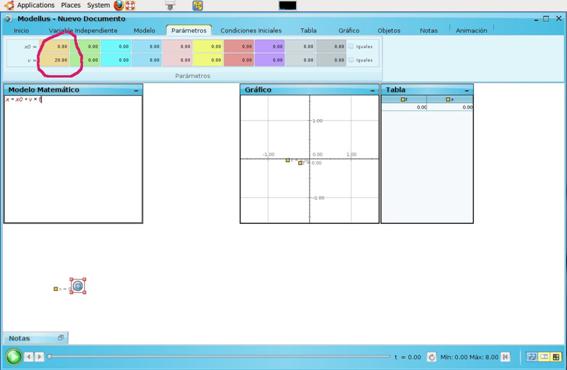
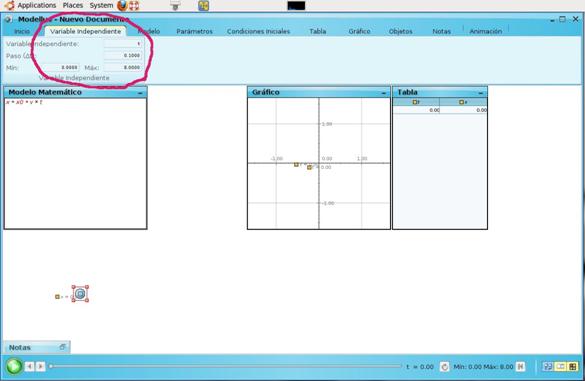
Con estos valores ya conocidos, el programa puede realizar el ciclo para la variable independiente tiempo, entre un valor inicial (mínimo) y un valor final (máximo), con un paso (Dt); todos estos valores se pueden asignar y variar en el menú  «Variable independiente». En el problema, cambiarán el valor final a 8 segundos.

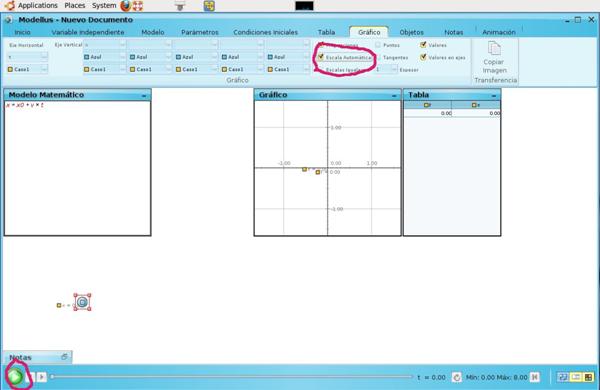
El programa mostrará al cuerpo moviéndose con una velocidad constante a medida que pasa el tiempo, y también generará una tabla con los valores para el tiempo y la posición, así como el gráfico correspondiente. En el menú «Gráfico», seleccionen la opción «Escala automática», para que realice el gráfico entre los extremos deseados, y luego aprieten el botón verde que está abajo a la izquierda, para comenzar la visualización.

El siguiente video muestra este resultado: MRU-Actividad 1 Modellus

2. En los procesadores de textos de sus equipos portátiles, realicen un informe detallado de lo realizado en esta actividad.

Actividad 2: Problema de encuentro en el MRU. Modellus

1. Resuelvan el tradicional problema de encuentro:

Un tren sale desde Buenos Aires hacia Mar del Plata a una velocidad constante de 60 km/h. Una hora más tarde, otro tren sale de Mar del Plata a una velocidad de 45 km/h. Tomando la distancia de Buenos Aires a Mar del Plata de 400 km, y considerando ambos movimientos como rectilíneos y uniformes, encuentren a qué distancia de Buenos Aires se cruzan ambos trenes.

a) Tomen un sistema de referencia con su origen en Buenos Aires. Realicen un diagrama con los trenes en sus posiciones iniciales, indicando sus velocidades como vectores.

b) Resuelvan el problema analíticamente.

c) Resuelvan el problema utilizando el programa Modellus. En el siguiente enlace, pueden ver el video con el ingreso del modelo matemático. Agreguen dos partículas que representen a los trenes, y relacionen sus posiciones con las variables creadas en el modelo. Asignen los valores iniciales en el gráfico y, en la tabla, agreguen la variable x2. Observen el enlace: video del encuentro en Modellus

2. En sus equipos portátiles, realicen un informe sobre lo realizado, incluyendo un listado de los programas utilizados y los resultados obtenidos.