Contenidos

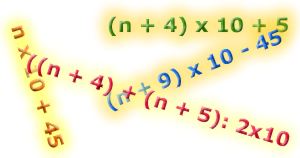
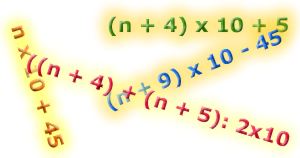
Modelización de situaciones problemáticas a través de fórmulas.

Propósitos

Se trata de una actividad que puede ser utilizada en los comienzos del Álgebra. La producción de fórmulas es un recurso interesante para la introducción de "las letras" en la clase de Matemática; en este caso, el recurso algebraico aparece como un medio para resolver problemas que implican la exploración de regularidades. Esta situación en particular es rica puesto que puede dar lugar a diferentes métodos de cálculos y, por ende, a una variedad de fórmulas que implicará una discusión sobre la validez y la equivalencia de las mismas.

Asimismo, la situación exige la puesta en funcionamiento de un proceso de generalización y abre un espacio para el trabajo sobre la problemática de la validación en la clase de Matemática, en particular, la validación de un proceso de generalización.

Desarrollo

Organización de la clase

Se arman equipos de cuatro alumnos y el docente propone el siguiente juego (en la Parte 1 del juego no se puede usar calculadora).

• Parte 1
  "El profesor les dará diez números consecutivos y el equipo que primero encuentre la suma de estos números será el ganador".
  El docente propone, a continuación, comenzar a jugar y escribe en el pizarrón:
  Primera partida: 19, 20, 21, 22, 23, 24, 25, 26, 27, 28.
  Luego de finalizada esta partida, se propone la segunda:
  Segunda partida: 783, 784, 785, 786, 787, 788, 789, 790, 791, 792.
  Luego de finalizada esta partida, se propone la tercera:
  Tercera partida: 6985, 6986, 6987, 6988, 6989, 6990, 6991, 6992, 6993, 6994.
• Parte 2
  Cada equipo tendrá un tiempo para buscar alguna estrategia que permita ganar rápidamente, cualquiera sean los diez números consecutivos que se propongan.
  Luego, cada grupo tendrá que presentar la estrategia diseñada y dar razones que justifiquen por qué ella sirve cualquiera sean los diez números consecutivos y por qué creen que permite ganar rápidamente.
  

Puesta en común

Al finalizar la Parte 2 se realiza una puesta en común en la cual se discuten las estrategias propuestas y se analizan aquéllas que supuestamente permiten ganar más rápido.

• Parte 3
  Se busca ahora escribir una fórmula que permita, dado el primero de los diez números consecutivos que hay que sumar, obtener como resultado la suma de éstos.
  Cada grupo tendrá que explicar cómo ha obtenido la fórmula.
  

Puesta en común

Se analizan, se comparan y se validan las diferentes producciones.

• Parte 4
  1. ¿Es posible que la suma de diez números consecutivos dé por resultado 735.245? ¿Por qué? Si la respuesta es afirmativa, ¿cuáles son los números que se han sumado?
  2. ¿Es posible que la suma de diez números consecutivos dé por resultado 18.450? ¿Por qué?
  Si la respuesta es afirmativa, ¿cuáles son los números que se han sumado?

Puesta en común

Se analizan, se comparan y se validan las diferentes producciones.

Comentarios

En la Parte 1, frente a una respuesta de un grupo, el docente controla el resultado de la suma. En caso de obtenerse una respuesta incorrecta, el juego continúa hasta que aparezca la primera respuesta correcta. En esta instancia no hay ningún tipo de discusión en relación a la manera de obtener los resultados (cada equipo no deberá divulgar la estrategia que supuestamente le permite ganar el juego).

En la primera parte de la situación, los números que se proponen son cada vez mayores, de tal manera que la realización de todas las cuentas comience a manifestarse como un método "poco económico" y así implicar al alumno en la búsqueda de otros procedimientos.

El hecho de no conocer de antemano el conjunto de números que el docente propondrá podría funcionar como "motor de generalización": las estrategias locales diseñadas en la primera parte (esencialmente ligadas a estrategias de cálculo mental) no son fácilmente generalizables, fundamentalmente frente a la exigencia de comunicación; muchas de ellas deberán reformularse a partir de la exigencia de la producción de una fórmula.

Es importante, en la Parte 3, discutir la equivalencia de diferentes fórmulas posibles, cada una de ellas proveniente de diferentes regularidades, como por ejemplo:

1. n x 10 + 45 siendo n el primer número de la secuencia
2. (n+9) x 10 - 45 siendo n el primer número de la secuencia
3. ((n+4) + (n+5)): 2 x 10 siendo n el primer número de la secuencia
4. (n+4) x 10 + 5 siendo n el primer número de la secuencia
5. 5x (2n+9) siendo n el primer número de la secuencia