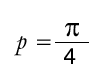Enigmas geométricos planteados a partir de una situación de juego.
Dos biólogos, la Dra. Grilly y el Dr. Cricri, están estudiando desde hace meses las costumbres de
una especie de grillos. Han podido localizar un grillo de este tipo en una parcela de campo en la pampa
húmeda, y observar que el grillo sale de su madriguera por la noche para alimentarse de alfalfa y regresa de
día. La madriguera es un agujero en la tierra y los científicos discuten respecto de la
ubicación exacta del grillo dentro de ella, pues se manejan con cierto grado de indeterminación debido
a irregularidades del terreno y a perturbaciones sonoras.
Los dos biólogos analizan mediciones vinculadas con la ubicación del grillo en su madriguera. Cada
uno enuncia una hipótesis: la Dra. Grilly afirma que está en el interior del rectángulo XYZW, de
1,5 m por 0,9 m. El Dr. Cricri, por su parte, estima su posición en el interior de una elipse inscripta en el
rectángulo XYZW, como indica la siguiente figura:

- Explicá, utilizando argumentos vinculados con figuras geométricas, por qué la elipse
representada en el dibujo está bien definida.
- Si aceptamos que la afirmación de la Dra. Grilly es correcta, ¿cuál es la probabilidad de
que la afirmación del Dr. Cricri sea también correcta? Describí los pasos que seguiste.
- Para que realices tu propia experiencia te proponemos organizar dos simulaciones que te permitirán
estimar la probabilidad teórica que antes calculaste:
- Proponé una simulación utilizando lentejas y el dibujo anterior y pautá los pasos a
seguir. (Tené en cuenta que las lentejas representan el grillo y su posición sobre el
gráfico, la ubicación en la madriguera.)
- Proponé una simulación por computadora y pautá los pasos a seguir.
- Llevá a cabo los experimentos que propusiste.
- Exponé las conclusiones a las que llegues comparando los resultados obtenidos en ambos casos.
Referencias curriculares
Las actividades corresponden a los siguientes contenidos:
Contenidos conceptuales
- Cónicas como lugar geométrico. Ecuaciones de cónicas.
- Experimentos aleatorios.
Contenidos procedimentales
- Cálculo de probabilidades.
- Simulación.
- Creación y desarrollo de estrategias para la resolución de problemas.
Materiales
Cada grupo o alumno (según lo decida el docente) deberá contar con:
- hojas de papel de tamaño suficientemente grande para realizar la experiencia,
- lentejas,
- hilo (si desea construir la elipse por el método del jardinero).
- Computadora. (Se puede realizar la actividad prescindiendo de la computadora, en este caso se simulará
la situación solamente con lentejas.)
Tiempo estimado
Un módulo de 80 minutos. (Sin embargo, el tiempo dependerá de la costumbre que tengan los alumnos
para resolver situaciones problemáticas.)
Comentarios y sugerencias
- Se trata de una situación problemática que permite enseñar conceptos geométricos
referidos a las cónicas, combinándolos con teoría de probabilidades. Además, propone la
creación y el desarrollo de experiencias de simulación.
- Podés proponerles a los alumnos que saquen fotos o filmen las distintas experiencias y luego editen un
video con Movie Maker (programa de edición de videos instalado en los
equipos). Si no cuentan con una cámara filmadora o de fotos, podrán utilizar las webcams que incluyen
los equipos o un celular con cámara de fotos. Los alumnos deberán organizarse en grupos y distribuir
los roles y tareas para realizar un trabajo colaborativo. Podrán compartir los archivos y documentos y
alojarlos en la red de la escuela o en alguna de las máquinas.
- Se combinan el análisis teórico de los datos y la simulación. Para el cálculo
teórico de la probabilidad de que la respuesta del Dr. Cricri sea correcta, se hace indispensable calcular
el área de la elipse. La propuesta con lentejas requiere el trazado de una cónica, mientras que en el
tratamiento informático de la experiencia se utiliza la ecuación analítica de la misma.
- La propuesta didáctica para estos contenidos (cónicas, probabilidades y simulación), que
ya han sido estudiados de manera separada, permite lograr una visión integradora de la matemática y
muestra los aportes de la disciplina para la resolución de situaciones problemáticas de cualquier
tipo.
- Se proponen dos alternativas, considerando los recursos disponibles. Uno de estos experimentos utiliza
únicamente lentejas, lo cual permite su realización en el aula; el otro usa recursos
informáticos, como la planilla de cálculo, o bien, en caso de que los alumnos posean nociones de
programación, el diseño de un programa sencillo. Para ello quizás resulte oportuno utilizar el
programa Euler Math Toolbox,
instalado en los dispositivos de los alumnos y en las notebooks de los docentes.
- En una etapa posterior, puede pensarse en un planteo de geometría tridimensional que use cuerpos
geométricos; por ejemplo, un elipsoide inscripto en un paralelepípedo.
- También es posible utilizar argumentos de análisis matemático para el cálculo de la
probabilidad de que el Dr. Cricri haya acertado, ya que es posible calcular las áreas mediante integrales
definidas.
- Otra modificación posible en la actividad puede consistir en un cambio de las dimensiones del
rectángulo. Será necesario, entonces, un cambio de escala para poder realizar la
experimentación.
- Cabe señalar que en los dispositivos de los alumnos y en las notebooks de los docentes hay instalados
graficadores de funciones matemáticas, realizadores de cálculos científicos y sistemas de
geometría dinámica, que pueden resultar de utilidad para esta actividad.
Adaptaciones de las actividades para grados superiores
Las actividades propuestas a partir de la situación problemática de las hipótesis sobre la
ubicación del grillo pueden adaptarse de varias maneras.
Una posible adaptación para la afirmación del Dr. Grilly es reemplazar la elipse por una
circunferencia, partiendo de un cuadrado, en lugar de partir de un rectángulo. En este caso, la pregunta
referida a la unicidad de la elipse apela a la definición de circunferencia y a las propiedades de los
cuadrados.
La actividad así planteada permite calcular aproximadamente el número p, a partir de las
simulaciones propuestas. La probabilidad p de que un punto del cuadrado, generado al azar, esté en el
círculo es igual al cociente entre el área del círculo y la del cuadrado:
Generando una cantidad suficientemente grande de pares ordenados es posible obtener un valor aproximado para el
número p.
Otra posible adaptación para el Tercer Ciclo de la EGB, si no se desea abordar el tema de las
cónicas, puede ser partir de otras figuras geométricas. Por ejemplo, reemplazar a la elipse por un
rombo:
Esta modificación puede conducir a un interesante tratamiento de las propiedades de los
cuadriláteros. Es posible incluso cambiar la posición de los vértices del cuadrilátero
interior para generar nuevos problemas.
Textos: Cecilia R. Crespo Crespo. Ilustración: Sergio Merayo. Edición: Christiane C.
Ponteville