Todo lo que vemos, registramos, conocemos, vivimos ... todo es finito. Sin embargo, hay una intuición de que el todo es inabarcable. Es la idea del infinito.

Infinito, eso es lo que raya

Imagen: Silvana Coratolo

Siempre se puede seguir un poco más. Quizá sea esa intuición la que nos incitó a abstraer el concepto de infinito. Siempre que haya un número habrá otro más grande que le sigue, eso lo sabemos aunque no tengamos un nombre para cada número.

Esta idea da origen al infinito de los números naturales; con ellos podemos contar cualquier cosa pero, ¿es este el único infinito? ¿Será el infinito de los continuos momentos que transcurren de un instante a otro, o los infinitos puntos del espacio, en definitiva el mismo infinito?

Adrián Paenza muestra en el programa Alterados por pi una forma de entender que dos segmentos tienen la misma cantidad de elementos. Sugerimos una guía de actividades que nos acerquen al  concepto de infinito, aquel que desafía permanentemente la intuición. Vean para empezar clip de video del programa.

(Ver capítulo completo)

Actividad 1: dos segmentos cualesquiera

Consignas

1. El segmento [0,1] tiene infinitos puntos.

   Para probar esto pueden tomar el punto medio de un intervalo y verificar que tal punto es menor que el extremo superior y mayor que el extremo inferior de tal intervalo. Así, tomando los puntos medios de los intervalos a que van quedando a la izquierda verán que 1/2, 1/4, 1/8,... son infinitos puntos distintos en el intervalo.

2. Una proyección.

   Proponemos ahora una posible biyección entre dos segmentos cualesquiera.

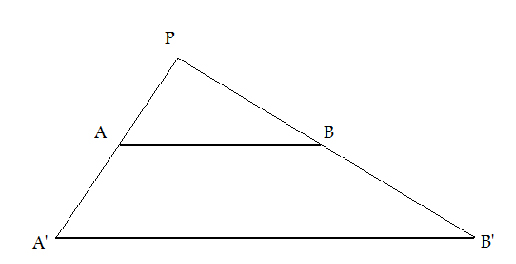
   Para eso, dibujen los dos segmentos paralelos distintos AB y A'B', tracen las rectas AA' y BB' como en la figura y llamen P a la intersección de tales rectas. Consideren la función del segmento AB en el segmento A'B' que corresponde a cada punto C del segmento AB con el único punto en el segmento A'B' que pertenece a la recta PC. Observen que tal función es una biyección.

Actividad 2: La circunferencia y la recta.

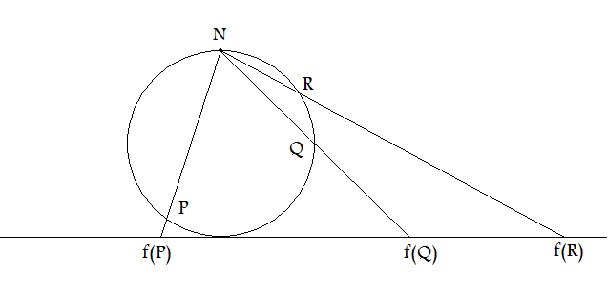
Uno podría preguntarse si estas dos figuras tan emblemáticas de la matemática pueden ponerse en biyección, veremos aquí un método que permite hallar tal función, será una proyección estereográfica la que nos resolverá el problema.

Consignas

1. Dibujen una circunferencia y tracen una recta tangente horizontal debajo de la misma. Llamen N al punto más alto de la circunferencia (norte). Noten que cada recta que pasa por N no horizontal corta a la circunferencia en un único punto distinto de N, y a la recta en un único punto.
2. Hallen una expresión para una función biyectiva entre la circunferencia de centro (0,1) y radio 1, sin el punto N=(0,2), y el eje de las abscisas.

Actividad 3: infinitos infinitos

Esta actividad tiene el propósito de probar que hay  infinitos distintos. Una manera de entender esto es viendo que hay dos conjuntos infinitos, A y B, tales que hay una función inyectiva de A en B pero que no hay ninguna función sobreyectiva. Esto claramente refleja que la cantidad de elementos de A es menor que la cantidad de elementos de B.

Consigna

Consideren los conjuntos N -correspondiente al de los números naturales- y S -formado por sucesiones de ceros y unos-. Por ejemplo, algunos elementos de S son (0101010101...), (00000...), (11111...), (10000...), (01000...), (00100...), etc.

1. Prueben que existe una función inyectiva de N en S.
2. Prueben que ninguna función de N en S es sobreyectiva.
3. Prueben que el conjunto S está en biyección con el conjunto formado por todos los subconjuntos de N.

Ayuda: empecemos con un ejemplo sencillo. Consideremos estas tres tiras, 001, 011 y 110, de sólo tres números e intentemos formar una cuarta tira formada también con los números 0 y 1, diferente de las otras tres.

Veamos cómo: pongamos las tiras una debajo de la otra

001

011

110

Tomemos de la primera tira el primer número, que es un 0. Si tomamos para la nueva tira un 1 como primer número, entonces será diferente de la primera. Como segundo número tomaremos uno diferente del segundo  número de la segunda tira, es decir, tomaremos un 0. Y con la tercera, por el mismo razonamiento, tomaremos un 1. Así obtenemos la tira 101, que será diferente a las otras tres.

A este procedimiento se le llama método diagonal: nos movemos a lo largo de la diagonal del listado tomando elementos diferentes a los de la diagonal, de esa manera nos aseguramos que la nueva tira es diferente a todas las de la lista. ¿Cómo podemos usar este método para resolver nuestro problema?

Nota: hay un conocido teorema de Cantor, con el que Cantor resuelve con toda generalidad el problema que acabamos de plantear y da una demostración de que hay infinitos infinitos distintos.

Actividad de cierre

Piensen en la escritura decimal de un número real en el intervalo [0,1] como tiras de dígitos. Dos tiras de dígitos distintas corresponderán a números distintos, en particular las tiras de ceros y unos se corresponden con algunos de estos números. Deduzcan por qué hay más números reales que naturales.

Encuentro Descargas

• Capítulo 6: Infinito, eso es lo que raya

Autor: Sebastián Freyre