
Euclides demostró que todo número natural podía factorizarse como producto de números particulares que se denominan números primos.¡Enterate de todo lo que hay que saber sobre los primos!

Adrián Paenza, en el programa del canal Encuentro, "Alterados por Pi", habla de estos números y de su importancia. En este clip de video del programa vemos que el hecho de que un número esté compuesto por muchos números primos dice que el número tiene muchos divisores. Pero, ¿cómo podemos contar la cantidad de divisores de un número?, ¿qué información nos da saber la factorización de un número? Y, finalmente, ¿qué podemos hacer para saber si un número es primo?
http://www.encuentro.gov.ar/Content.aspx?Id=2646
| (Ver capítulo completo) |
Otra pregunta muy oportuna sería cuántos números primos hay, nuevamente fue Euclides quien probó, en la misma época en que demostró el Teorema Fundamental de la Aritmética, que los primos son infinitos, con una demostración tan bella como sencilla.
En esta actividad vamos a sugerir dos formas de averiguar si un número es primo. La primera sólo responde si el número dado es primo y la segunda, llamada Criba de Eratóstenes>, además nos da un listado de todos los primos menores a él.
El primer método consiste en dividir al número dado por todos los números menores o iguales a su raíz cuadrada, si ninguno de los cocientes es entero se puede deducir que el número es primo. Esto se debe a que, si el número tiene algún divisor mayor a su raíz cuadrada, entonces el cociente entre éstos es otro divisor que es menor o igual a su raíz cuadrada.
El segundo método, la Criba, consiste en escribir todos los números entre 2 y el número dado, llamémoslo n, e ir eliminando de la lista aquellos que son múltiplos de dos, salvo al dos, luego a los de tres, salvo el tres, luego a los de cinco (que es el primero que había quedado en la lista), salvo el cinco y así siguiendo. Si n fuera primo quedaría en la lista, si no en algún momento hubiera sido eliminado.
Por ejemplo, para n=20 sería así:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 3 | X | 5 | X | 7 | X | 9 | X | 11 | X | 13 | X | 15 | X | 17 | X | 19 | X |
| 2 | 3 | X | 5 | X | 7 | X | X | X | 11 | X | 13 | X | X | X | 17 | X | 19 | X |
| 2 | 3 | X | 5 | X | 7 | X | X | X | 11 | X | 13 | X | X | X | 17 | X | 19 | X |
Discutan sobre cuál de los dos métodos es más eficiente para decidir si un número es primo ¿La velocidad es la única ventaja?
Como es sabido, los números primos tienen exactamente dos divisores positivos, 1 y él mismo. Esta actividad está asociada a conocer la cantidad de divisores positivos que tiene un número entero. Por ejemplo 12 y 18 tienen la misma cantidad porque 12=22.3 y los divisores son de la forma 2i.3j con i igual a 0, 1 ó 2 y j igual a 0 ó 1. Mientras que en 18 están intercambiados los roles de 2 y 3.>
Discutan ntre todos cuáles fueron los resultados obtenidos. Observen que la cantidad de divisores de un número no tiene relación con su tamaño, si no con su factorización.
Les proponemos el siguiente juego de ingenio en el que la factorización es una herramienta clave para resolverlo.
Escriban en cada casilla de la pirámide un número natural mayor que 1 de modo que:
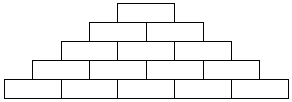
Discutan acerca de la importancia de los números primos y la factorización de números enteros. Consideren cuestiones prácticas; por ejemplo: ¿sería más difícil organizar la vida si un día tuviera 23 horas y un año 13 meses? ¿Por qué usamos docenas?
Autor: Sebastián Freyre