Existen solo cinco poliedros regulares, pero infinitos polígonos regulares. ¿Por qué? ¿Cuáles son los secretos de estas interesantes figuras geométricas?

Para adentrarnos en el tema de los polígonos regularesles proponemos ver el siguiente clip de video en el cual Adrián Paenza muestra una forma muy simpática de construir algunos de ellos.

(Ver capítulo completo)

Quizá sea su geometría simple, hecha de segmentos, o su simetría y regularidad o tal vez la forma en que se aproximan al círculo cuanto más lados tienen pero todos estos hechos singulares los distinguen. Por eso, una de formas de hallar aproximaciones de la longitud de una circunferencia es calculando longitudes de polígonos regulares siempre del mismo radio pero con cada vez más lados.

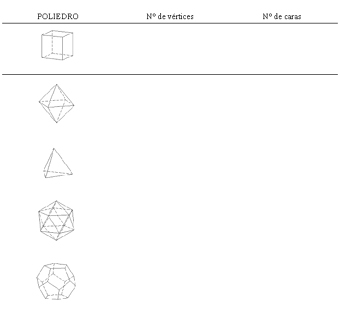
Si quisiéramos calcular la superficie de una esfera con la misma técnica estaríamos condenándonos al fracaso, desde hace 2400 se sabe que esto es imposible, lamentablemente, hay sólo cinco tipos de poliedros regulares, también llamados sólidos platónicos. Vamos a conocerlos.

Actividad 1

En un poliedro regular, en cada vértice, la suma de los ángulos de los polígonos que concurren en él es menor a 360°, que corresponde al giro completo. En base a esto, respondan:

1. ¿Qué polígonos regulares se pueden usar para formar poliedros regulares?
2. ¿Serían capaces de fabricar un poliedro que tenga como caras los polígonos que mencionaste arriba?. Inténtenlo.
3. A diferencia de lo que ocurre con los polígonos regulares que son infinitos, hay sólo pocos tipos de poliedros regulares. ¿Te animarías a decir cuáles son todos ellos?

Cierre

Discutan sobre los resultados; de ser posible construyan en cartulina los cinco poliedros regulares.

Actividad 2: los poliedros y sus parejas

Los poliedros regulares están de alguna manera apareados. Esta actividad esta propuesta para entender el singular comportamiento de los poliedros regulares. Incluso Kepler les dedicó mucha atención e intentó con algo cercano al éxito inscribir las órbitas de los planetas en ellos y, recíprocamente, a ellos en las órbitas planetarias.

Consigna:

1. A cada uno de los 5 poliedros que figuran a continuación, colóquenles el número de vértices y el número de caras.

   

2. ¿Observan algún patrón en las anotaciones que acaban de hacer? ¿Qué números se repiten?
3. Con cada uno de los poliedros regulares construyan otro poliedro de la siguiente manera: marquen los puntos medios de cada cara del poliedro y trazen un segmento entre dos de ellos si estos son adyacentes (es decir si comparten una arista). ¿Qué poliedro resulta en cada caso?

4. Discutan sobre esta particularidad de los poliedros regulares

   Nota : por esta razón decimos que el icosaedro es el poliedro dual del dodecaedro, que el cubo es dual del octaedro y que el tetraedro es dual de si mismo.

   Actividad de cierre

   Discutan sobre la diferencia que hay entre polígonos y poliedros regulares resaltando que hay infinitos de los primeros pero sólo cinco de los segundos. Observar que la circunferencia es una figura regular que se puede aproximar con poliedros regulares y que la esfera, que también es regular (podría pensarse como un poliedro de infinitas caras cuyos ángulos sólidos son todos planos), no puede aproximarse por poliedros regulares.

   Encuentro Descargas

   • Capítulo 13: Polígonos y poliedros regulares

   Enlace de interés

   • Kepler, los planetas y los poliedros regulares.

   Autor: Sebastián Freyre.