Elaboración de conjeturas y pruebas.
La siguiente actividad está pensada con el propósito de que los alumnos elaboren conjeturas y las
prueben.
Se ha elegido plantearla en un contexto geométrico referido a la relación entre perímetro y
área de rectángulos. Su resolución puede poner de manifiesto errores resistentes de los alumnos
(algunos creen que varían de igual modo) que suelen persistir aún en el Nivel Polimodal.
En las propuestas para el aula Nº 1 y Nº 8 hemos considerado la variación del área de cuadriláteros de perímetro fijo. En esta ficha estudiaremos la relación entre los perímetros de rectángulos de área fija.
La situación permite ser modelizada por medio de funciones. La determinación del valor mínimo del perímetro remite a considerar el problema de encontrar un valor extremo.
Considerá todos los rectángulos de igual área, por ejemplo de área 36 cm 2 . ¿Cómo varía el perímetro?
Es recomendable un primer momento de trabajo individual. Es posible que algunos alumnos respondan que el perímetro no varía y que otros, apoyándose en dibujos como los siguientes, afirmen lo contrario:
Una pequeña puesta en común que permita a los distintos grupos argumentar a propósito de sus repuestas permitirá concluir que el perímetro varía.
En esta instancia resulta adecuado preguntar:
De los rectángulos anteriores: ¿existe alguno de perímetro mínimo? Justificá.
La respuesta a esta pregunta posibilita plantear dos funciones:
=> f(x) = 36/x (que expresa cómo varía una dimensión del rectángulo
en función de la otra).
=> f(x) = 2(x + 36/x) (que expresa como varía el perímetro del rectángulo en
función de una de sus dimensiones).
En el caso de esta última función, y a fin de simplificar el trabajo, puede considerarse el semiperímetro: f(x) = x + 36/x.
Un estudio de las correspondientes gráficas resulta pertinente:
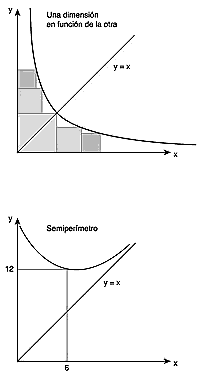
El análisis de la gráfica de la izquierda permite observar la simetría de esta última con relación a la recta de ecuación y = x. Asimismo pone en evidencia que si una de las dimensiones tiende a infinito, la otra tiende a cero, por lo que el área permanece constante. Esto puede relacionarse con el estudio de las asíntotas de la hipérbola, las rectas de ecuación x = 0 e y = 0.
El análisis de la otra gráfica muestra que cuando una de las dimensiones del rectángulo
tiende a in-finito, el semiperímetro también lo hace. En este caso las asíntotas son x =
0 e y = x.
Si los alumnos dibujan rectángulos como los sombreados, es posible que conjeturen que el rectángulo de
menor perímetro es el cuadrado. Resulta entonces pertinente preguntar porqué.
Una posible prueba consistiría en el planteo de la inecuación:
x + 36/x 
12 o sea 
0
Luego, como x es positivo, se tiene (x - 6)2 0, lo que implica que el mínimo alcanzado es 12 para de la x =
6.
En caso que los alumnos dispongan noción de derivada como así también de procedimientos
elementales de cálculo de las mismas (por definición, por reglas), esta situación puede
utilizarse para abordar o profundizar el estudio de los valores extremos de una función.