Applet 1: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 2: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 3: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 4: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 5: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 6: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 7: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Applet 8: situaciones dinámicas relacionadas con el llenado de un recipiente con agua, y la realización del gráfico respectivo. Se pueden modelizar con funciones lineales y cuadráticas.

Recomendaciones para el docente

Instrucciones de uso y propiedades de los applets

• En todos los gráficos se representa en el eje horizontal el tiempo que permanece abierta la canilla y en el vertical, la altura que alcanza el agua en la botella.
• Para obtener el trazado de las variables en cada simulación, cliquear en la flecha azul (debajo del gráfico), que representa la apertura de la canilla, y en la flecha roja, el vaciado de la botella.
• Para volver a empezar, cliquear el botón "inicio".
• Para cambiar la escala y los valores máximos de los ejes horizontal y vertical, utilizar las flechas que están en la parte superior del gráfico (escala, 0.x y 0.y, respectivamente).
• En los applets 1, 2 y 3 se puede cambiar el ancho de la botella arrastrando el punto rojo R para la derecha o la izquierda.
• En los applets 4 a 8 se puede cambiar la forma de la botella arrastrando los puntos rojos.
• Para observar las coordenadas de un punto en el gráfico, cliquear sobre el mismo.

Análisis didáctico: Propuesta de utilización de los applets en el aula

Armar, preferentemente, grupos de 2 o 3 alumnos por computadora.

Parte 1

Plantear el siguiente problema:
Se llena una botella con agua. Para ello se abre una canilla que arroja siempre el mismo caudal de agua y se cierra sola cuando la botella está llena. La botella tiene forma cilíndrica y se representa con un rectángulo.

Representar en un par de ejes cartesianos la altura que alcanza el agua en la botella en cualquier tiempo después de abrir la canilla. Pensar cómo será este gráfico, y dibujar un esquema aproximado.

Comentarios

Se espera que los alumnos puedan anticipar que la gráfica comienza en (0;0) y que asciende hacia la derecha, es decir que es una función creciente.

Parte 2

Utilizar el applet 1 y comparar el gráfico esquemático de la Parte 1 con el observado en la pantalla.

Luego de analizar las diferencias, contestar, en grupos, las siguientes preguntas:

1. ¿Por qué el gráfico es un segmento de recta y no una curva?
2. ¿Podría ser una línea discontinua?
3. ¿Cuánto tiempo se necesita para llenar la mitad de la botella? ¿Y la cuarta parte?
4. ¿Cuál es la velocidad de llenado de la botella?
5. Si la velocidad de llenado fuera mayor, ¿cómo sería el gráfico?
6. Si inicialmente la botella no estaba completamente vac ía, ¿cómo sería el gráfico?
7. ¿Cuáles podrían ser las causas de la modificación de la velocidad de llenado?

Comentarios

• Para poder determinar que el gráfico es un segmento de recta (pregunta a), un argumento posible sería que, debido a la forma de la botella y considerando que la canilla arroja siempre la misma cantidad de agua, a iguales períodos de tiempo corresponden iguales aumentos de altura de agua en la botella.
  
• El objetivo de la pregunta c es poner en evidencia, a partir del gráfico, que la relación planteada es directamente proporcional.
• Al responder la pregunta d se espera que los alumnos puedan relacionar la velocidad de llenado de la botella con la inclinación de la recta en el gráfico. Es muy útil trabajar con los pares ordenados que se pueden obtener al cliquear sobre puntos de la recta.
• Las preguntas d y e permiten relacionar la constante de proporcionalidad con la velocidad de cambio de altura del agua en la botella.
• Para responder la pregunta f, seguir los siguientes pasos que permiten obtener el gráfico de llenado de una botella, que inicialmente no estaba completamente vacía, con el applet 1:
  1. Cliquear en "config", en la esquina superior derecha del gráfico.
  2. Cliquear en la flecha de la pestaña blanca que dice "<applet>", en la parte superior derecha, y seleccionar "FUNCIONES".
  3. En la ventana que aparece, introducir "+2" luego de la primera palabra "caudal". Debería quedar:
     h=ind(x>0)*(x*caudal+2/base)*(1/ind(t*caudal<base*alto)).
  4. Cliquear en el botón "prueba".
  5. Iniciar el programa. Si en lugar de poner +2 se pone otro valor, el trazado del gráfico comenzará en otro lugar.

En este gráfico se podrá verificar que aunque la velocidad de llenado permanece constante, la relación entre el tiempo y la altura del agua en la botella no es directamente proporcional.

También resulta útil, para analizar la relación, el recurso de obtener las coordenadas de los puntos de la recta.

Parte 3

1. Actividad de anticipación
   Plantear la siguiente situación para resolver en grupos:
   Si se utiliza la misma canilla, que arroja siempre el mismo caudal de agua, pero una botella más ancha, ¿cómo se modificaría el gráfico? ¿Ysi fuera más angosta?
   
   Realizar un gráfico de cada una de las situaciones y compararlo con el de la situación planteada en las Partes 1 y 2. Describir y explicar las diferencias observadas.
2. Actividad para validar anticipaciones
   Proponer la exploración del applet 2 , en el cual se puede simular el llenado de botellas con diferentes anchos. En el caso de existir diferencias entre las predicciones y los gráficos generados con el applet, pedir a los alumnos que expliquen las posibles razones y en el caso de que coincidan las anticipaciones y los gráficos generados con el applet, que expliquen los motivos de las decisiones adoptadas para realizar las anticipaciones.

Parte 4

Plantear el siguiente problema para resolver en grupos:
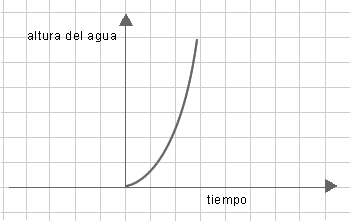
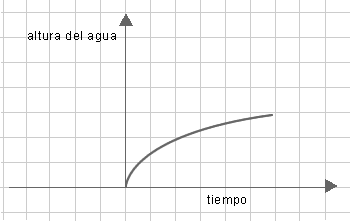
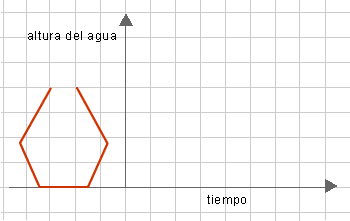
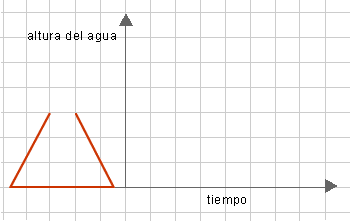
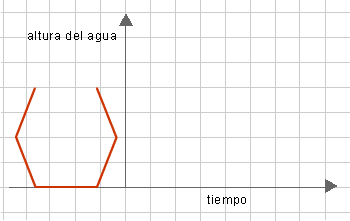
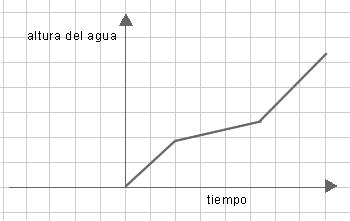
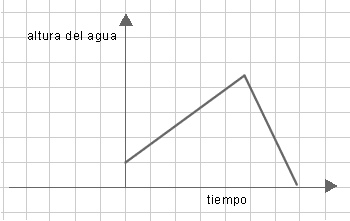
¿Cuáles serían las formas de las botellas con las que se podrían generar gráficos de llenado (altura que alcanza el agua en la botella en función del tiempo con la canilla abierta) con formas similares a los gráficos que se muestran a continuación?

Luego de resolver el problema, solicitar que elijan entre los applets 5 y 6 , los correspondientes para validar las respuestas y analizar las razones de posibles diferencias.

A continuación, se les puede dar un tiempo a los alumnos para que escriban las conclusiones a las que llegaron comparando las formas de las botellas con los gráficos respectivos.

Puesta en común
Solicitar a cada grupo de alumnos que lea sus conclusiones a los demás. Organizar un debate en el que se confronten, analicen y validen las producciones de los grupos.

Comentarios

• Se espera que los alumnos puedan relacionar la forma de la botella con el gráfico que representa la altura que alcanza el agua en la misma cuando se llena. Para ello, hay que tener en cuenta que en las partes más anchas, la altura va aumentando a menor velocidad y la curva es más horizontal que en las partes más angostas, donde la altura va aumentando a mayor velocidad y la curva es más vertical.
• Es importante discutir con los alumnos las razones por las cuales la curva es suave, y no una sucesión de segmentos articulados que van cambiando la inclinación. También pueden deducir qué forma debería tener la botella para que la curva fuera de este tipo.
• Otra posibilidad consiste en proponer preguntas similares a las de la Parte 2 (c a f). De esta manera, los alumnos podrán darse cuenta de que, en algunos casos, la velocidad de cambio de altura no es constante y de que tampoco se cumple la proporcionalidad directa.
• Los applets 5 y 6 , además de utilizarse para validar las producciones de los alumnos, deberían servir como instrumentos para la exploración y la búsqueda de razones para explicar las posibles discrepancias entre las anticipaciones y los gráficos generados por los applets.

Parte 5

Plantear el siguiente problema:
Se desea vaciar la primera botella una vez que se llenó completamente. Para ello, se dispone de una bomba que hace salir el agua por una canilla que arroja siempre el mismo caudal de agua. ¿Cómo sería el gráfico que representa la altura del agua en la botella en función del tiempo transcurrido desde que se empezó a vaciar?

Puesta en común
Recolectar las producciones de los grupos y dibujarlas en el pizarrón. Permitir que los alumnos se tomen cierto tiempo para comparar y justificar sus producciones.

Comentarios

• Se espera que los alumnos argumenten que la línea del gráfico debe empezar desde la altura máxima de la botella y debe ser decreciente. Como la velocidad de vaciado es constante, la línea del gráfico debe ser un segmento de recta. El punto donde corta el eje de las x informa sobre el momento en que se terminó de vaciar.
• Es interesante vincular este gráfico con el de llenado y que los alumnos observen que son simétricos, como si se invirtiera la lectura de los valores de la altura.

Parte 6

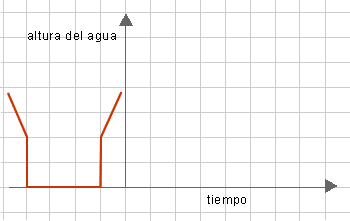
Explorar los applets 7 y 8 y luego resolver las siguientes actividades.

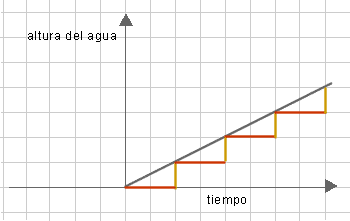
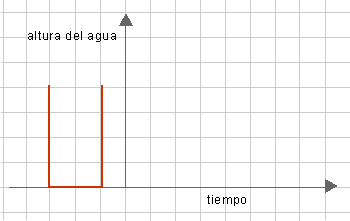
1. Dibujar los gráficos que corresponden al llenado y al vaciado de las botellas con las siguientes formas.
   
2. 
3. 
4. 
5. 
6. Considerar una botella igual a la primera de la actividad a. ¿Qué situaciones podrían representar cada uno de los siguientes gráficos?
   
7. 

Comentarios

El objetivo de esta actividad es combinar las conclusiones a las que se han llegado a lo largo de toda la secuencia presentada.

Objetivos didácticos

Que los alumnos:

• Reconozcan que el gráfico correspondiente al llenado de una botella depende de su forma pero no es igual a la misma.
• Analicen la relación que existe entre la forma de la botella y el gráfico que representa la altura del agua en función del tiempo, tanto en el llenado como en el vaciado.
• Relacionen un gráfico rectilíneo con el crecimiento uniforme de la altura del agua, lo cual ocurre cuando las paredes laterales de la botella son verticales.

Contenidos

• Análisis de gráficos cartesianos.
• Construcción de un gráfico a partir de otro.
• Concepto de función: dependencia y variación.
• Proporcionalidad directa.
• Lectura e interpretación de información matemática.

Objetivos

• Identificar las variables de una función y describir la forma en que una varía respecto de la otra.
• Relacionar los gráficos con la situación que representan.
• Construir gráficos que representen variaciones de una situación.
• Construir un gráfico a partir de otro.
• Reconocer problemas vinculados al concepto de proporcionalidad directa.

Autoras: Viviana Firbank, Claudia Comparatore, Silvia Altman