Tiro oblicuo

	Autor: Hernán Ferrari Responsable disciplinar: Silvia Blaustein Área disciplinar: Física Temática: Movimiento general de un cuerpo sobre la superficie de la Tierra Nivel: Secundario, ciclo básico Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

Sobre un cuerpo que se mueve en el aire en las cercanías de la superficie de la Tierra, actúa solamente la fuerza peso en la dirección vertical (despreciando el rozamiento con el aire). Como la fuerza peso es una fuerza uniforme, esto es, tiene en todas las posiciones la misma dirección, el mismo módulo y el mismo sentido, en la dirección vertical existe una aceleración constante y el movimiento será un MRUV. Por su parte, en la dirección horizontal no hay fuerzas, con lo cual el movimiento horizontal será un MRU. La velocidad en esa dirección será constante, con un valor igual a la componente inicial de la velocidad en la dirección horizontal. Por esta razón, el movimiento está limitado a un plano, definido por la vertical y la componente de la velocidad inicial en la dirección horizontal.

Tomando un sistema de coordenadas con un eje x en la dirección horizontal y un eje y en la dirección vertical, se tendrá en el eje x un MRU, con las relaciones:

  con  constante;

y en el eje y, considerando la aceleración de la gravedad hacia abajo de un módulo igual a 10 m/s², se obtendrá:

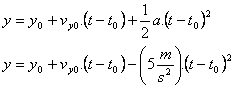 para la coordenada y mientras que

Objetivo de las actividades

Que los alumnos analicen el movimiento de un cuerpo bajo la acción de la fuerza gravitatoria sobre la superficie de la Tierra considerando una velocidad inicial con una componente horizontal no nula.

Actividad 1

Resuelvan el siguiente problema de tiro oblicuo: Se arroja un cuerpo formando un ángulo de 45 grados, con una velocidad inicial tal que las componentes horizontal y vertical son iguales a 70 m/s.

a) Encuentren la altura máxima que alcanza el cuerpo. ¿En qué instante de tiempo llega a esa posición?

b) ¿Cuál es el alcance horizontal del tiro?

c) Resuelvan el problema analíticamente y con la utilización del software Modellus. En el último caso, obtengan las respuestas a las preguntas planteadas observando la tabla de valores.

d) Ingresen los lápices necesarios para graficar las posiciones y las velocidades en función del tiempo.

Video: Tiro oblicuo

e) Con el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Incluyan los programas utilizados y los gráficos realizados.

      Este enlace permite descargar un archivo de la aplicación Modellus: Tiro oblicuo 1

Actividad 2

El siguiente es un problema clásico de encuentro entre un tiro oblicuo y una caída libre: Si se lanza un proyectil contra un blanco que se deja caer libremente, apuntado en la dirección en la que lo impactaría en ausencia de la gravedad, dicho proyectil lo impactará independientemente de la velocidad inicial. Esto será así porque la magnitud del desplazamiento, debido a la gravedad, será la misma tanto en el tiro oblicuo como en la caída libre.

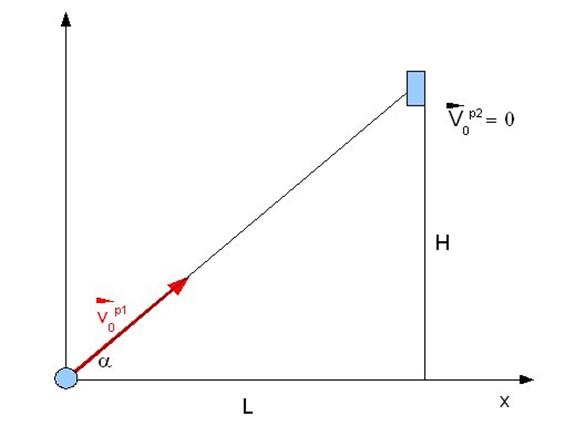
Ambos cuerpos comienzan sus movimientos en el mismo momento (t = 0 segundos). La partícula 1 está en el origen elegido de las coordenadas, y la partícula 2, a una distancia horizontal L y a una altura H, comenzando una caída libre, esto es, desde el reposo.

a) Considerando el sistema de referencia mostrado en la figura anterior, construyan el modelo matemático  para cada partícula con el programa Modellus.

b) La componente horizontal y la vertical de la velocidad inicial pueden obtenerse por trigonometría, utilizando las distancias L y H. Realicen la visualización en el Modellus para distintos valores del módulo de la velocidad inicial de la partícula 1, y verifiquen que, independientemente de esta velocidad, las partículas siempre se encuentren. Consideren que la partícula 2 está a 10 metros de altura y a una distancia de 15 metros en la dirección horizontal.

c) Con el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Incluyan los programas utilizados y los gráficos realizados.

      Este enlace permite descargar un archivo de la aplicación Modellus: Tiro oblicuo 2

Actividad 3

Resuelvan el siguiente problema de tiro oblicuo: Se arroja un cuerpo formando un ángulo de 30 grados, con una velocidad inicial de módulo 3 m/s.

a) Visualicen el problema utilizando el Modellus.

b) Agreguen un vector que corresponda a la velocidad del cuerpo durante el tiro oblicuo.

c) Calculen la aceleración, y con ella calculen también la aceleración tangencial y la centrípeta, recordando que la primera está en la dirección de la velocidad y la segunda es perpendicular a esta. Agreguen dos vectores que muestren estas aceleraciones siguiendo la partícula.

d) Consideren la relación entre la aceleración centrípeta y el cuadrado del módulo de la velocidad para obtener la curvatura de la trayectoria del tiro oblicuo. Para ello, grafiquen el módulo de la aceleración centrípeta en función del cuadrado del módulo de la velocidad.

e) Con el procesador de textos de sus equipos portátiles, elaboren un informe detallado de todos los pasos realizados en esta actividad. Incluyan los programas utilizados y los gráficos realizados.