Sistemas de ecuaciones, parte I
 |
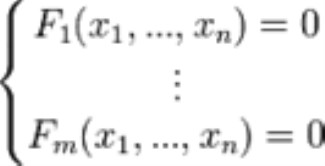Autores: Laura Spivak y Pablo J. Kaczor
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Ecuaciones
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
Los sistemas de ecuaciones intervienen en diversas situaciones que nos rodean, por ejemplo, en los problemas de encuentro.
En este curso, te proponemos abordar el tema aprovechando las ventajas de los programas que permiten hacer simulaciones con animaciones, en este caso, la aplicación Modellus. También se usará la aplicación Geogebra, para representar los sistemas de ecuaciones que se plantearon y para comprobar las respuestas dadas.
Objetivo de las actividades
Promover el uso de programas que permitan realizar animaciones de modelos matemáticos y de programas graficadores; la discusión y el intercambio de diversas estrategias entre pares; el trabajo colaborativo; la realización en conjunto de la propuesta; la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Actividad 1
Pidan a sus alumnos que se reúnan de a dos para discutir ideas, aunque cada integrante trabajará con su equipo portátil (si el número de alumnos es impar, puede haber un grupo de tres). Para realizar la actividad, usarán el programa Modellus.
1) Abran el programa Modellus, que permite producir simulaciones animadas de modelos físicos, realizar gráficos y generar tablas de valores. La situación para resolver es la siguiente:
Martina empieza a correr sobre una pista hasta adquirir una velocidad constante de 3 m/s, que logra mantener. Pone en marcha su cronómetro y en ese mismo instante, su perrito, situado a 42 m de ella, viene corriendo a su encuentro, con la misma velocidad constante que Martina. ¿Cuántos segundos marcaba el cronómetro cuando se cruzaron? ¿En qué posición estaban al cruzarse?
La ecuación que determina la posición de un cuerpo que marcha con velocidad constante (MRU), en función del tiempo, es:
p0 es la posición inicial;
v es la velocidad constante;
t es el tiempo;
y t0 es el tiempo inicial.
¿Cuál es la ecuación que le corresponde a Martina? ¿Y al perrito?
Discútanlas y anótenlas en la ventana Modelo Matemático, cuidando que no se repitan los nombres de las variables dependientes. Para ello, llamen p1 a la posición de Martina y p2 a la del perrito. Recuerden no dejar espacios y usar * como símbolo de multiplicar.
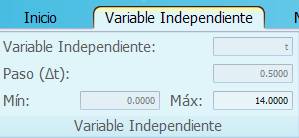
- En la pestaña Variable Independiente pongan los datos que se muestran a continuación.
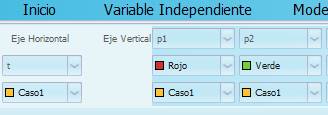
- En la pestaña Gráfico, revisen que aparezcan todas las variables: t, p1 y p2. Tilden Proyecciones y Valores en los ejes. Elijan además un color para cada gráfico. Por ejemplo:
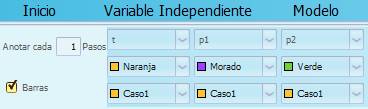
- En la pestaña Tabla, verifiquen que aparezcan todas las variables, tilden Barras y elijan un color para cada variable. Por ejemplo:
- Para que se produzca la animación, en la pestaña Objetos introduzcan una partícula y en Apariencia elijan Corredora. Pongan estos datos:
Repitan los pasos para introducir el perro, con estos datos:
- Coloquen los dibujitos debajo del gráfico como se muestra a continuación:
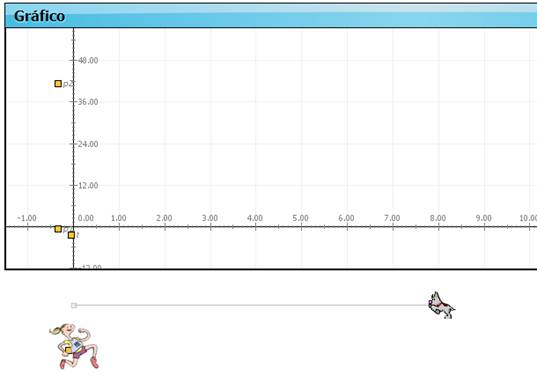
También pueden agregar un cronómetro. Para ello, en la pestaña Objetos, hagan clic en Analógico y luego en algún lugar en blanco de la ventana. Se abrirá la pestaña Animación. En esa pestaña, pueden poner estos valores y elegir los colores que prefieran:
- Presionen el botón verde y observen la animación. Recuerden que pueden usar el deslizador para visualizar las coordenadas de los puntos y otros detalles de interés:
- En la ventana Notas, redacten un breve informe explicando cuál es el sistema de ecuaciones que corresponde a la situación, qué tipo de sistema de ecuaciones es (compatible, incompatible o indeterminado) y las respuestas del problema planteado. Indiquen también qué significado tienen la pendiente y la ordenada al origen de cada una de las rectas del gráfico en el contexto del problema.
- Guarden el archivo con el nombre “Encuentro_Martina_perro”.
- Resuelvan ‘a mano’ el sistema de ecuaciones correspondiente y comprueben que la solución coincida con la que brinda el gráfico.
Actividad 2
Indiquen a sus alumnos que, de ser posible, se agrupen de la misma forma que cuando realizaron la actividad 1, y que continuarán con una actividad similar, también con la aplicación Modellus.
1) Abran el archivo que guardaron al finalizar la actividad 1.
2) Hagan las modificaciones en la ecuación del perrito considerando ahora que, en lugar de estar a 42 m de Martina y correr a su encuentro, sale 2 segundos después de que ella puso en marcha el cronómetro, para perseguirla con la misma velocidad.
3) Coloquen los dibujitos debajo del gráfico como se muestra a continuación:
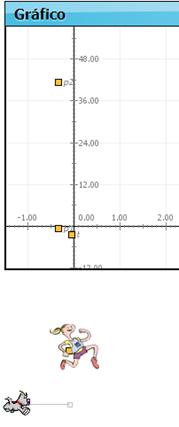
4) Presionen el botón verde y observen la animación.
5) En la ventana Notas, expliquen qué sucede esta vez; indiquen cuál es el sistema de ecuaciones correspondiente y qué tipo de sistema es el de este caso.
6) Guarden el archivo con el nombre “Perro_persigue_a_Martina”.
7) Resuelvan ‘a mano’ el sistema de ecuaciones correspondiente y comprueben que la solución coincida con la que brinda el gráfico.
Actividad de cierre
1) Accedan aquí y hagan doble clic sobre la actividad planteada con GeoGebra.
2) Muevan los puntos de los deslizadores hasta lograr que las rectas representen las ecuaciones que corresponden a Martina y el perrito, en los dos casos planteados.
La ecuación de Martina es: a • x + b • y = c
La ecuación del perrito es: h • x + j • y = k
3) Verifiquen si las soluciones que encontraron con Modellus y ‘a mano’ coinciden con las que visualizan con GeoGebra.
4) Guarden el archivo de GeoGebra en sus equipos y en el servidor.