Parábola
 |
Autores: Sebastián Vera, Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Estudio de la parábola como lugar geométrico
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
El matemático griego Menecmo (que vivió aproximadamente en el 350 a. C.) fue el primero en descubrir las parábolas. Pero fue Apolonio (262-190 a. C.), otro matemático griego, el primero en estudiar las curvas cónicas y encontrar la propiedad plana que las definía. Apolonio descubrió cómo se clasifican las cónicas y demostró también que las curvas cónicas tienen muchas propiedades interesantes.
Objetivos de las actividades
Reconocer la forma de la parábola.
Manejar e interpretar sus ecuaciones y propiedades más características.
Identificarlas en diferentes contextos cuando aparecen como lugares geométricos.
Reconocer la importancia de las cónicas en la ciencia y en la técnica.
Parábola
La parábola se define como un lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.
Los elementos de una parábola son:
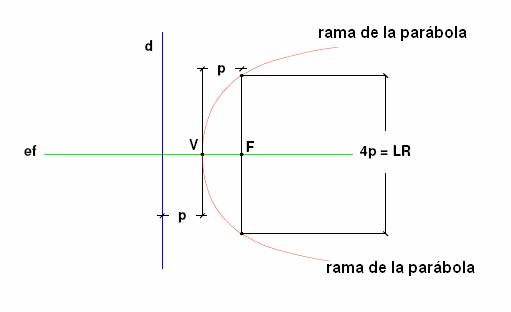
Vértice (V): Punto de la parábola que coincide con el eje focal.
Eje focal (ef): Línea recta que divide simétricamente a la parábola en dos ramas y pasa por el vértice.
Foco (F): Punto fijo no perteneciente a la parábola y que se ubica en el eje focal al interior de las ramas de la misma y a una distancia p del vértice.
Directriz (d): Línea recta perpendicular al eje focal que se ubica a una distancia p del vértice y fuera de las ramas de la parábola.
Distancia focal (p): Distancia entre vértice y foco, así como entre vértice y directriz.
Actividad 1
Ecuación de una parábola cuyo eje vertical es de la forma
y = 4 p x2 ; y = x2
La ecuación de una parábola cuyo eje horizontal es de la forma
x = 4 p y2 ; x = y2
1) Teniendo en cuenta las ecuaciones de las parábolas antes mencionadas, y haciendo uso del programa graficador (Geogebra), representen gráficamente las siguientes parábolas:
a) x = 2y2
b) y = 2x2
2) ¿Los gráficos son iguales? Justifiquen su respuesta.
3) En la vida cotidiana aparecen muchos ejemplos de gráficos de parábolas. En general, estos gráficos se relacionan con el concepto de función cuadrática. Observen el siguiente video, en el cual aparecen diferentes situaciones en las que interviene la función cuadrática y su gráfica, la parábola.
4) Mencionar por lo menos 5 ejemplos que hayan visto en el video anterior.
Actividad 2
1) Se dice que Arquímedes (287-212 a. C.) logró incendiar las naves romanas durante la defensa de Siracusa usando espejos parabólicos. Investiguen en Internet o en manuales y enciclopedias sobre este hecho y expliquen en qué consistió y qué propiedades parabólicas se aplicaron para quemar las naves.
2)Dadas las siguientes ecuaciones:
y = 2x2
x = 2y2
Grafiquen en el programa GeoGebra y determinen si ambas funciones se cortan en uno o dos puntos. De ser así, ¿cuáles son esos puntos? (para una mejor visualización en el programa, utilicen la función zoom y para la intersección de las curvas utilicen la función intersección de dos objetos, así podrán obtener valores con mayor precisión).
Actividad de cierre
1)Utilizando el programa GeoGebra, disponible en sus equipos portátiles, grafiquen la siguiente parábola: y = (x + k)2 donde k toma valores desde -3 hasta 3.
a) Describan qué efecto se produce en el gráfico cuando la variable k toma valores diferentes.
2) Utilizando el programa GeoGebra, disponible en sus equipos portátiles, grafiquen la siguiente parábola: y = x2 + h donde h toma valores desde -3 hasta 3. Describan qué efecto se produce en el gráfico cuando la variable h toma diferentes valores.
3) Junto con sus compañeros y el docente, discutan y saquen conclusiones sobre lo observado.
Enlaces de interés y utilidad para el trabajo
Cónicas, lugares geométricos: la parábola