Operaciones con números reales
 |
Autores: Daniel Brizuela, Javier Peña y Sebastián Vera
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Operaciones matemáticas
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
La resolución de ejercicios matemáticos nos ofrece diferentes posibilidades de técnicas, de caminos para alcanzar el resultado. Tal vez, lo más simple sea tomar una calculadora y realizar el cálculo sin necesidad de preguntarme si el resultado es correcto.
En la presente actividad, trabajaremos con expresiones matemáticas en la que intervienen números reales. Encontraremos entonces, números enteros, decimales y/o fraccionarios y números irracionales. El objetivo es desarrollar estrategias de resolución con expresiones exactas.
Objetivo de las actividades
- Reflexionar sobre el trabajo desde el concepto de la exactitud.
Actividad 1
Operar en el campo de los números reales significa trabajar con exactitud, con expresiones que indiquen con precisión el número que interviene en una operación, en especial los números irracionales que derivan de la expresión de raíz (√). Cuando el número esté expresado en este modo: √2; √5; 2√7; etc., lo denominaremos número radical.
Aprender a trabajar con estas expresiones significa trabajar con exactitud. Es nuestra intención avanzar en este concepto. Por este motivo no convertimos estas expresiones en números decimales, ya que de ese modo estaríamos trabajando con aproximaciones que son números inexactos.
1) Resuelvan las siguientes operaciones. Para hacerlo, utilicen la calculadora científica que está instalada en sus equipos portátiles.
a) 6 √3 + 4 √3 - 7 √3 =
b) ½ √5 - ¾ √5 + 2/3 √5 =
c) 0,4 √13 - 1,6 √13 + 2,24 √5 =
2) Comparen los resultados obtenidos con los demás compañeros. ¿Todos obtuvieron los mismos resultados?
Actividad 2
1) Analicen los resultados de las siguientes operaciones:
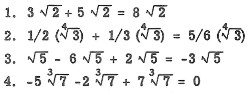
2) Utilicen la calculadora disponible en sus equipos portátiles para verificar el resultado.
3) ¿A qué conclusiones pueden arribar sobre la suma y resta de radicales semejantes?
4) Aplicando las conclusiones obtenidas en el punto anterior, resuelvan las siguientes operaciones con radicales semejantes, pero ahora sin utilizar la calculadora.
a) 6√3 + 4√3 - 7√3 =
b) ½√5 - ¾ √5 + 2/3√5 =
c) 0,4√13 - 1,6√13 + 2,24√5 =
d) -2√3 + 5√3 - 6√3 =
e) 10√343 - 1/3√7 - ½√63 =
5) Verifiquen los resultados obtenidos utilizando la calculadora.
Vemos que sumar y restar es posible empleando propiedades precisas de las operaciones con números reales. También podríamos multiplicar y dividir en el campo de la exactitud, retomando propiedades ya conocidas. Para ello recordamos propiedad distributiva en la radicación:

A partir de propiedades conocidas, podemos operar sin dificultad con números radicales. La condición que se cumple en estos casos es que mantienen el mismo índice. Entonces, si leemos en forma inversa estos ejemplos, estamos multiplicando o dividiendo con radicales.
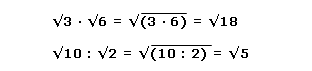
En este sentido, aplicando otra propiedad de la multiplicación, la propiedad conmutativa (“el orden de los factores no altera el producto”), podremos resolver operaciones más complejas:
3 √3 5 √6 = 3 . 5 √3 √6 = 15 √18
Asimismo, respetando propiedades de la división:
8 √10 : 2 √2 = 8 : 2 √10 : √2 = 4 √5
Esta base teórica funciona como disparador para profundizar la resolución de ejercicios con números radicales.
Actividad 3
- 1) A través de Internet, enciclopedias o manuales, investiguen sobre las operaciones con radicales y sus propiedades. Una vez obtenida la información, elaboren una tabla en el procesador de textos disponible en sus equipos portátiles. Complétenla mostrando ejemplos de operaciones con radicales e indicando las propiedades utilizadas en cada operación.
- 2) A partir de lo investigado, traten de pensar alguna situación o problema de la vida cotidiana en el que tengamos que operar con radicales. Describan y redacten la situación y muestren la o las operaciones que intervendrían para resolver el problema.
- 3) Comparen su propuesta con la de algún compañero.
Actividad de cierre
Otro número real (irracional) con el cual podemos trabajar el tema de la exactitud es el famoso número pi (ח).
1) Calculen, como ejemplo, cuánto vale el perímetro de una circunferencia con un diámetro de 2 cm. Recuerden que el perímetro de una circunferencia está dado por la siguiente expresión:
perímetro = diámetro · ח |
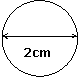 |
a) Comparen los resultados obtenidos con los demás compañeros
b) Si queremos trabajar con exactitud, ¿cómo quedará expresado el resultado?
2) Calculen el valor exacto de la medida en centímetros del “ecuador” de una pelota de fútbol de 21,8 cm de diámetro.
a) Ahora trabajen con una pelota cuyo radio mide 1 cm más que la anterior y hallen el valor exacto de la diferencia entre las medidas de los dos “ecuadores”.
Links de interés y utilidad para el trabajo
Radicales (números irracionales)