Números complejos, números imaginarios

	Autor: Fernando Luis Maffuche Responsable disciplinar: Sebastián Vera Área disciplinar: Matemática Temática: Números complejos Nivel: Secundario, ciclo orientado Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

Los números imaginarios surgieron al intentar encontrar las soluciones a las ecuaciones del tipo .

El propósito de esta actividad es que los alumnos interpreten la importancia de conocer el conjunto numérico: números complejos. Que descubran que con ellos se pueden resolver situaciones que con otros conjuntos numéricos no es posible. A la vez, que investiguen también sus aplicaciones en las distintas áreas.

Objetivos de las actividades

• Brindar información a través de nuevas tecnologías.
• Investigar y trabajar sobre el conjunto numérico: números complejos, con el propósito de estimular la reflexión crítica.
• Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
• Promover el uso de distintos programas en el área de la Matemática.
• Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
• Relacionar temas de formación general con las distintas áreas del conocimiento.

Objetivos pedagógicos

Actividad 1

1) Resuelvan las siguientes ecuaciones:

2) Luego, respondan las preguntas que están a continuación:

a) ¿Las ecuaciones anteriores tienen solución en el conjunto de los números reales? ¿Por qué?

b) ¿Se les ocurre alguna solución para las ecuaciones anteriores?

c) Si intentan resolver la raíz cuadrada de menos uno con la calculadora, ¿qué ocurre?

Para resolver las ecuaciones que se presentan a continuación, deben conocer el conjunto de los números complejos, también llamados imaginarios.

3) Donde la definición inicial es:

Los matemáticos italianos Gerolamo Cardano y Rafael Bombelli se encontraron con el problema que presentamos en los casos anteriores. Entonces Bombelli optó por la definición: .

Ahora podrán resolver las ecuaciones anteriores de manera correcta.

Actividad 2

Una forma de expresar un número complejo es la binómica: , siendo a la parte real, y b, la imaginaria.

Estos números se pueden representar en el plano cartesiano:

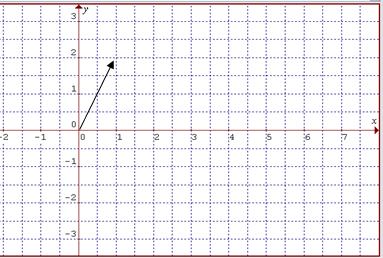
En el gráfico anterior se representó el número imaginario: .

Siempre la primera componente se representa en el eje x, y la segunda, en el eje y.

1) A continuación, representen los siguientes números complejos:

2) Pueden imprimir un plano cartesiano, utilizando el software Graphmática, para facilitar el trabajo.

Actividad 3

Este conjunto numérico también se utiliza en el área eléctrica, por ejemplo, en el tema impedancia.

La impedancia es lo que se opone al paso de la corriente alterna. Se mide en Ohm. Posee una componente resistiva (R) y una componente reactiva (X).

Z = R + jX

1) Investiguen cómo se suman los números complejos en forma binómica, para poder saber cuál es el resultado de la asociación de impedancias, presentada a continuación:

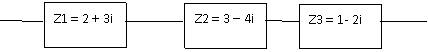
2) Para finalizar, les proponemos que investiguen en Internet o en otras fuentes, cómo se expresan los números complejos en forma polar o trigonométrica. Luego grafiquen los siguientes números complejos en papel de calcar, utilizando la misma escala: Za = 4 + 3i y Zb = 5 . (Cos 37° + i.Sen 37°).

3) Superpongan ambos gráficos y respondan:

a) ¿Cómo son los gráficos?

b) ¿A qué conclusión pueden llegar?