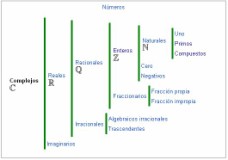
Números complejos
 |
Autores: Daniel Brizuela y Javier Peña
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Conjunto de números complejos
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
Los números complejos surgen como necesidad de resolver un problema hasta aquí sin solución: la raíz de índice par de un número negativo. Este nuevo conjunto numérico permite resolver cuestiones prácticas que antes no tenían solución o tenían tratamientos complejos. A lo largo de esta secuencia los alumnos trabajarán con diferentes propuestas que los acercarán a comprender la necesidad de crear un nuevo conjunto numérico.
Objetivos de las actividades
Que los alumnos:
infieran la lógica de la construcción de los campos numéricos en general y el campo de los números complejos en particular;
comprendan el concepto de unidad imaginaria;
comprendan el concepto de número complejo.
Objetivos pedagógicos
Actividad 1
1) Si tenemos una calculadora que solo resuelve operaciones en el campo de los números naturales (N):
a) ¿Cuáles de las siguientes operaciones se podrían realizar?
8 + 2 =
2 - 8 =
8 - 2 =
8 : 2 =
2 : 8 =
b) ¿Por qué hay operaciones que no se pueden hacer con la calculadora? ¿Cómo podríamos resolver este problema?
c) Ahora, si tenemos otro tipo de calculadora que permite la resolución de operaciones en el conjunto de los números enteros (Z), ¿podrían resolver todas las operaciones dadas en el ítem a? Indiquen cuáles no se podrían resolver y justifiquen su respuesta.
d) Y si la calculadora solo pudiese resolver operaciones en el campo de los números racionales (Q), ¿qué impedimento operativo tendría?
2) Propongan una operación matemática que no se pueda resolver con la calculadora que resuelve operaciones en el campo de los números racionales. Justifiquen su respuesta y discutan las actividades realizadas con el docente.
Para reforzar lo trabajado hasta aquí, observen y analicen el siguiente video:
Actividad 2
Ahora bien, por suerte nuestras calculadoras actuales operan en el conjunto de los números reales (R). Realicen operaciones matemáticas con la calculadora provista en sus computadoras portátiles.
1) ¿Existe alguna operación matemática que no pueda resolverse con nuestra calculadora? Traten de calcular las siguientes raíces y saquen una conclusión sobre ese tipo de operaciones.
i) √1=
ii) √-1=
iii) 3√-1=
iv) 4√-1=
2) En grupos de dos o tres alumnos, investiguen en Internet, manuales o enciclopedias la forma en que la matemática ha resuelto este problema.
3) Utilizando el procesador de textos instalado en sus equipos portátiles y con la información obtenida en la investigación, redacten un resumen en el que respondan las siguientes cuestiones:
a) ¿Quién o quiénes fueron los primeros matemáticos que trabajaron con el problema de calcular raíces cuadradas de números negativos?
b) ¿En qué otras situaciones o aplicaciones aparece este problema?
c) ¿Cómo resolvieron este problema?
Actividad 3
En la actividad anterior trabajaron con un problema que llevó muchos años de trabajo y que condujo a crear un nuevo conjunto numérico: el conjunto de números complejos. Este nuevo conjunto nos permite calcular cualquier raíz de índice par de radicando negativo. Por ejemplo, si queremos calcular la siguiente raíz: 
, la idea es escribir el radicando en producto de dos o más factores numéricos, y luego aplicar la propiedad distributiva de la radicación respecto de la multiplicación.
= 
= 
. 
= 2 i
1) Siguiendo la misma idea, completen el siguiente cuadro:
|
Raíz a resolver |
Factores del radicando |
Propiedad distributiva |
Resultado |
|---|---|---|---|
 |
|||
 |
|||
|
|||
 |
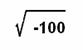
Para profundizar sobre este tema, visiten los siguientes links:
Números complejos, en Escolared
Actividad de cierre
1) Utilizando el programa Geogebra, grafiquen la parábola que resulta de la siguiente función cuadrática: f(x) = x2 - 2x + 2
a) ¿La parábola obtenida corta al eje de las x? ¿Qué sucede con las raíces?
b) Calculen las raíces igualando la función a cero: 0 = x2 - 2x + 2 y aplicando la fórmula resolvente para la ecuación de segundo grado. ¿Qué conclusión pueden extraer?
c) ¿Qué particularidad tienen las raíces complejas halladas en el ítem anterior? Discútanlo junto con el docente.
d) Investiguen en Internet cuáles son las distintas formas de representar los números complejos. Escriban un ejemplo y muestren al menos tres formas de expresar este número.
Enlaces de interés y utilidad para el trabajo
Números complejos, en Wikipedia
Números complejos, en Escolared