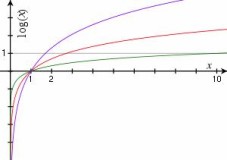
Logaritmos y cambio de base

	Autores: Weber Rodrigo, Javier Peña y Daniel Brizuela Responsable disciplinar: Sebastián Vera Área disciplinar: Matemática Temática: Aplicación de cambio de base para resolver operaciones con logaritmos en diferentes bases Nivel: Secundario, ciclo orientado Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

En esta secuencia trabajaremos con la propiedad de cambio de base de los logaritmos. En la primera actividad se propone que los alumnos investiguen la utilidad de los logaritmos a lo largo de la historia. En la segunda actividad formalizaremos el concepto de cambio de base destacando su utilidad y aplicaciones. En la actividad de cierre trabajaremos con la propiedad de cambio de base, aplicándola en ejercicios matemáticos.

Objetivos de las actividades

Que los alumnos:

Interpreten la historia de la matemática y la relacionen con los logaritmos.

Desarrollen el concepto y las aplicaciones de cambio de base a través de investigaciones.

Apliquen en distintos casos el cambio de base para asimilar el concepto.

Utilicen el cambio de base para operar con los logaritmos en distintas bases.

Actividad 1

En el siglo IX, en Arabia, se escribieron los primeros libros sobre el juego de ajedrez. Uno de los autores de estos libros fue Al-Adlí. Su obra titulada El libro del ajedrez narra la célebre leyenda de los granos de trigo, en la cual se le atribuye la invención del ajedrez a un campesino llamado Sissa Ben Dahir.

1) Visiten la siguiente página web. Lean cuál es la relación que se da entre la leyenda de los granos de trigo y los logaritmos.

a) A partir de lo leído, expliquen brevemente qué sucedió con los granos de trigo y cómo se puede relacionar el cálculo propuesto con los logaritmos.

b) Expliquen con sus palabras qué significa calcular el logaritmo de un número. Den por lo menos cinco ejemplos.

2) ¿Qué bases utiliza la calculadora para calcular el logaritmo de un número? ¿Qué diferencias hay entre esas bases? Utilicen la calculadora científica, instalada en sus equipos portátiles, para mostrar algunos ejemplos de aplicación.

Actividad 2

En la actividad anterior analizaron las bases con las que trabaja una calculadora. Ahora, respondan:

1) ¿Será posible calcular los siguientes logaritmos utilizando la calculadora?

● Log₂ 154

● Log₃ 123,58

● Log₇ 1.203,58

Existe una propiedad de los logaritmos que nos permite transformar un logaritmo dado en cierta base en otro logaritmo expresado en una base que nos resulte más simple para llegar a su solución, por ejemplo, aquellas que aparecen en las calculadoras científicas (el ln o el log en base 10). Esta propiedad se denomina cambio de base.

2) Para comprender cómo se aplica la propiedad cambio de base, ingresen al siguiente link.

3) Apliquen lo analizado en el ítem anterior para calcular los logaritmos dados en el ítem 1. Para ello, utilicen la calculadora científica instalada en sus equipos portátiles.

4) Analicen la demostración de esta propiedad junto con su docente y desarróllenla en sus carpetas.

Actividad de cierre

1) Resuelvan los siguientes logaritmos:

• Sabiendo que log 25 = 1,397940, calcular ln 25.
• Sabiendo que log₂ 8 = 3, calcular log₁₆ 8
• Sabiendo que log₃ 27 = 3, calcular log₉ 27
• Sabiendo que log 2 = 0,301030 y log 7 = 0,845098, calcular log₇ 2
• Sabiendo que log 3 = 0,477121 ,Calcular log₃ 10

2) Apliquen un cambio de base que resulte conveniente para obtener los siguientes logaritmos con la calculadora que tienen instalada en sus equipos portátiles, y anoten los valores redondeados al milésimo.

a) log₂ 18=

b) log₃ 100=

c) log_0,1 25=

d) log₇ 63=

e) log₂ 20=

Enlaces de interés y utilidad para el trabajo

Logaritmos

Logaritmos, por Silvia Sokolovsky

Funciones exponencial y logarítmica

Enciclopedia de logaritmos - Ecuaciones exponenciales

Webgrafía recomendada

Logaritmo, en Wikipedia