Interpretación y aplicación del concepto de derivada
 |
Autores: Laura Spivak y Pablo Kaczor
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Derivada
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
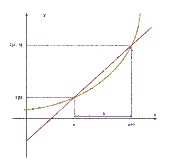
El concepto de derivada está presente cada vez que se produce un ritmo de cambio. Podemos verlo en el movimiento de los automóviles, en la caída de objetos, en una frenada brusca, en el aumento de una especie animal, en la superficie cubierta a medida que se va pintando una pared, y la lista es prácticamente interminable.
En este curso te proponemos abordar el tema aprovechando las ventajas de los programas graficadores GeoGebra y Modellus, y de material multimedia.
Objetivos de las actividades
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Objetivos pedagógicos
Actividad 1
Pídanles a sus alumnos que, reunidos en grupos de dos o tres, discutan ideas, aunque cada integrante trabajará con su equipo portátil.
Indíquenles que para realizar la actividad usarán el programa GeoGebra y el procesador de textos (donde responderán las preguntas que se formulan). Deberán tener los dos programas abiertos.
Sigan estos pasos:
- Abran el programa GeoGebra y el procesador de textos.
- En el programa GeoGebra, escriban la fórmula de una función polinómica de tercer grado. Por una cuestión de comodidad, que 4, 7 y 9 sean raíces de la función (pueden escribir la fórmula en forma factorizada). No es obligatorio que los integrantes del grupo escriban la misma fórmula.
- Pinten de azul el gráfico de esa función (vamos a llamarla función azul).
- Hagan que GeoGebra escriba la fórmula de la función derivada de la función azul.
- Pinten de rojo el gráfico de la función derivada (vamos a llamarla función roja).
1) ¿Qué forma tiene el gráfico de la función roja? ¿Por qué?
b) Copien la fórmula de la función roja en el Campo de Entrada, iguálenla a 0 y pulsen la tecla Enter.
c) Se habrá generado así una ecuación c; píntenla de verde.
2) Observen las rectas verdes que aparecieron: ¿qué muestran?
d) Marquen un punto cualquiera que pertenezca al gráfico de la función azul.
e) Tracen por ese punto la recta tangente al gráfico de la función azul. Para ello, usen la herramienta que se muestra a continuación:
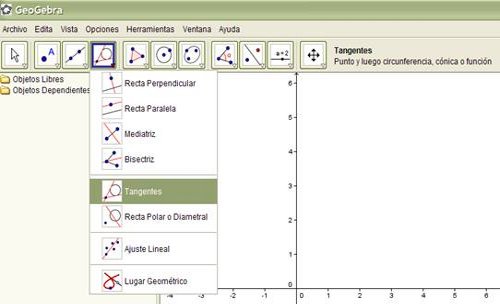
f) Muevan el punto recorriendo el gráfico y observen qué sucede con la recta tangente.
g) Hagan que GeoGebra muestre las pendientes de las rectas tangentes que aparecen. Para ello, usen la siguiente herramienta:
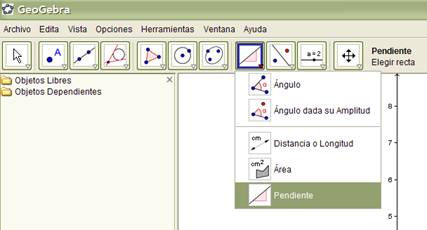
h) Vuelvan a mover el punto recorriendo el gráfico de la función y observen cómo varía el valor de la pendiente.
3) ¿Qué sucede con el signo de la pendiente para valores del dominio que están entre las rectas verdes? ¿Y para los valores que están a la izquierda o a la derecha de ese intervalo? ¿Cómo pueden explicarlo?
4) ¿Cuánto vale la pendiente cuando el valor del dominio coincide con la ecuación de cualquiera de las rectas verdes? ¿Por qué es así?
i) Modifiquen el valor del coeficiente principal en la fórmula de la función azul y generen así otra función (pueden probar incluso con un valor negativo para el coeficiente principal).
j) Hagan que el programa escriba la fórmula de la función derivada de esta última, y observen qué sucede con los gráficos.
k) Repitan los últimos dos pasos.
5) ¿A qué conclusión pueden llegar en cuanto a la variación del valor del coeficiente principal y a los gráficos que se generan?
Solicítenles a sus alumnos que guarden sus producciones con sus nombres y apellidos en el servidor, para su posterior evaluación.
Actividad 2
Propónganles a sus alumnos que miren con atención los siguientes videos cortos, en el orden indicado. En total son 13 videos y verlos todos lleva unos 25 minutos. Están narrados en español (de España) con mucha claridad. Después de verlos, deberán realizar una actividad que será evaluada.
Los videos son parte de una colección, realizados por California Institute of Technology & The Corporation for Community College, financiados por la Annenberg / CPB Project y producidos por Caltech e INTELECOM (un consorcio sin fines de lucro de los colegios comunitarios de California).
1- Caída libre en el vacío (2:33 min)
2- MRUV (2:02 min.)
3- La distancia en el MRUV (1:56 min)
4- El problema de la velocidad media (2:26 min)
5- La velocidad instantánea (2:20 min)
6- La velocidad como derivada de la distancia (1:38 min)
7- La aceleración como derivada de la velocidad (1:41 min)
8- Es como una síntesis de lo visto hasta acá y presenta g (2:40 min)
9- Concepto de derivada (2:26 min)
10- Concepto de pendiente (1:04 min)
11- Concepto de pendiente en un punto (1:30 min)
12- Concepto de derivada como límite (1:59 min)
13- El cuenta kilómetros como máquina de derivar (0:31 min)
Luego de ver los videos sugeridos, pídanles a sus alumnos que formen grupos de a dos o de a tres; que lean la situación que se plantea y que realicen los pasos que se indican.
Situación: Se dejó caer un objeto desde la terraza de un edificio de más de cien pisos, y se registraron los datos que muestra la tabla (están redondeados):
|
x |
f(x) |
|---|---|
|
Tiempo en el aire (s) |
Distancia recorrida (m) |
|
0 |
0 |
|
1 |
5 |
|
2 |
20 |
|
3 |
45 |
|
4 |
80 |
1) Abran el programa GeoGebra y carguen la tabla en la hoja de cálculo.
2) Seleccionen los pares de valores y hagan que se cree una lista de puntos; de esa manera, quedarán marcados los 5 puntos en el sistema de ejes cartesianos (de ser necesario, ajusten la escala de cada eje para visualizar los 5 puntos).
3) Determinen la fórmula de la función que contiene esos puntos y escríbanla en el campo de entrada, llamando x a la variable independiente. Pinten el gráfico de f(x) con azul, y consideren solo x ≥ 0.
4) Hagan que el programa escriba la fórmula de la función derivada de f(x). Pinten el gráfico de g(x) con rojo.
5) Respondan las siguientes preguntas en el procesador de textos:
a) ¿Qué representa la función g(x) en la situación planteada?
b) ¿Cuánto vale la pendiente de la recta roja? ¿Qué significado tiene ese valor?
6) Marquen un punto A en el gráfico de f(x), tracen la tangente a la curva por ese punto y hagan que se muestre el valor de la pendiente (m).
7) Muevan el punto A haciéndolo coincidir con P1, P2, P3, P4 y P5; observen cuánto vale m en cada caso y completen, en el procesador de textos, una tabla como la que se muestra en el ejemplo a continuación:
|
Punto |
Valor de la pendiente de la recta tangente al gráfico de f(x) en ese punto (m) |
g(x) |
|---|---|---|
|
P0 = (0, 0) |
g(0) = |
|
|
P1 = (1, 5) |
g(1) = |
|
|
P2 = (2, 20) |
||
|
P3 = |
||
|
P4 = |
8) Redacten las conclusiones que saquen al observar la tabla.
9) Hagan que el programa escriba la fórmula de la función derivada de g(x). Pinten el gráfico de h(x) con verde.
10) Expliquen qué representa la función h(x) en la situación planteada.
11) Guarden la producción en el servidor, con sus nombres.
Actividad de cierre
Pídanles a sus alumnos que formen grupos de a cuatro, y coméntenles que van a preparar una modelización de la caída libre de un cuerpo utilizando el programa Modellus.
1) En la ventana Modelo Matemático, escriban las fórmulas de:
d: distancia recorrida por el cuerpo a medida que va cayendo;
v: velocidad que adquiere mientras cae;
g: aceleración con la que cae (considerando la aceleración de la gravedad igual a 10 m/s²);
h: –f.
2) Ajusten los valores de la variable independiente, estableciendo un paso adecuado, desde 0 hasta 4, o más.
- En la ventana Tabla, activen Barras y asignen un color para t, d, v, g y h.
- En la ventana Gráfico, asignen a d, v y g los mismos colores que en la tabla, y hagan los ajustes de escala en los ejes que sean necesarios.
- En la pestaña Animación, elijan el modelo del objeto que cae (manzana, pelota, bola, partícula) y asignen Coordenada Horizontal (0) y Vertical (h), con escalas 1 y 5, respectivamente. Pidan que deje una marca cada 1 paso.
- Visualicen la animación y, en la ventana Notas, escriban una explicación clara y concisa que describa el fenómeno en términos matemáticos y físicos.
- Guarden el archivo con sus nombres en el servidor.
Enlaces de interés y de utilidad para el trabajo
Derivadas de las funciones f(x) = k • x, f(x) = sen x, f(x) = cos x (Video; 1:17 min)
Derivada de la suma (Video; 1:17 min)
Derivada del producto y de f(x) = xn (Video; 2:53 min)
La regla de la cadena (Video; 0:58 min)