Funciones trigonométricas, parte 2

	`Autores: Ana Verónica Veltri y Martín Miguel Pérez` `Responsable disciplinar: Sebastián Vera` `Área disciplinar: Matemática` `Temática: Funciones trigonométricas` `Nivel: Secundario, ciclo orientado` `Secuencia didáctica elaborada por Educ.ar`

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

En esta secuencia se abordarán los siguientes temas: aplicación de las funciones del tipo a la generación de sonidos, e interpretación de los parámetros que intervienen en la fórmula de la función.

Para emplearlo es necesario que los alumnos manejen las funciones trigonométricas con ángulos expresados en radianes. Antes de realizar las actividades, pueden reforzar los fundamentos matemáticos de esta aplicación con la secuencia “Funciones trigonométricas I” (ver secuencia “Funciones trigonométricas I”).

En este recurso se trabaja con los programas GeoGebra y Scilab.

Antes de comenzar, cabe aclarar que se trabajará sobre la base de la función , aunque en este caso se llamará t (tiempo) a la variable. Además es conveniente recordar la relación entre , el período T y la frecuencia f, de manera de expresar a . De este modo, la función puede escribirse como: , para visualizar la frecuencia en la fórmula.

Objetivos de las actividades

Promover la discusión y el intercambio de diversas estrategias entre pares.

Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Objetivos pedagógicos

Actividad 1

Esta actividad se dividió en tres partes: la primera, en la que se pueden “escuchar” las variaciones producidas por los cambios en la amplitud y la frecuencia; las otras dos permiten dar sentido a la suma de dos funciones periódicas.

Un coro trigonométrico

Aunque podemos escuchar bajo el agua, en general podría decirse que el sonido es aire en movimiento o, más específicamente, “aire en vibración” (Rojo, 2007).

El sonido se propaga generando oscilaciones periódicas en el aire. Por eso es útil usar funciones trigonométricas para representarlo.

Si la frecuencia de oscilación se encuentra entre los 20 Hz y los 20.000 Hz, nuestros oídos captan esa vibración del medio y el cerebro la interpreta como sonido.

Para ver (o mejor dicho, escuchar) qué efectos tienen sobre el sonido resultante las variaciones de los distintos parámetros de una función trigonométrica, pueden utilizar el Scilab como generador de audio. Recuerden que al emplear este programa, después de cada instrucción (o sentencia) que ingresen, deben apretar Enter. ¡Y no olviden el punto y coma al final, en las sentencias que así lo indiquen!

Pueden darles a sus alumnos las siguientes indicaciones:

Primero, ingresen la duración del tono, por ejemplo, 4 segundos. Para ello escriban la sentencia:	t = soundsec(4);
Luego, ingresen la función que generará la señal tomando, por ejemplo, f = 220 Hz:	y = 1sin(2%pi220t);
Para reproducir la función, se usa la siguiente sentencia:	playsnd(y)

¿Qué ocurre al apretar Enter después de la última sentencia? ¿Qué sucederá si se cambia algún parámetro?

Para “escuchar” la variación que se produce con un cambio en la amplitud, pueden ingresar una nueva función en el programa, por ejemplo, con amplitud 0,5 (no olviden darle otro nombre pues, si vuelven a ingresarla como y, perderán la función anterior).

¿Cómo queda expresada la nueva función?

También pueden expresarla como producto de 0,5, por la función anterior.

Para reproducir la función en este caso se escribe:

playsnd(0.5*y)

¿Qué resultado tiene en la señal de salida un cambio en la amplitud? Pueden probar con otras amplitudes, pero para que la señal no se distorsione y se escuche el tono correctamente, utilicen amplitudes no mayores a 1.

Ahora provoquen un cambio en la frecuencia. Para ello ingresen una nueva función, por ejemplo: f = 440 Hz.

La sentencia que deben ingresar es:	w = 1sin(2%pi440t);
Para reproducir la función usen la sentencia:	playsnd(w)

¿Qué escuchan? ¿Qué relación guarda el tono generado por y con el generado por w?

Para volver a escuchar los tonos generados y compararlos, pueden ingresar: playsnd(y), playsnd(0.5*y) o playsnd(w), dependiendo de lo que quieran escuchar.

Seguramente habrán captado el interés de sus alumnos, especialmente de los amantes del sonido. Se puede aprovechar este interés para ver qué ocurre con la señal producida por la suma de otras dos. Así que sin borrar ninguna de las sentencias ingresadas, continúen…

Batiendo

Generen una nueva señal cuya diferencia en frecuencia respecto de y sea de unos pocos hercios, por ejemplo: f = 230 Hz.

Ingresen la función que generará la señal, y a continuación, la sentencia para reproducirla:

z =1*sin(2*%pi*230*t);

playsnd(z)

Pídales al programa que reproduzca la suma y + z:

playsnd(y+z)

¿Qué escuchan? Investiguen qué nombre recibe el fenómeno generado.

Los sonidos del silencio

¿Qué sucedería si se reproducen simultáneamente dos funciones de igual amplitud y frecuencia, pero desfasadas π radianes?
Prueben ejecutando los siguientes comandos:

Ingresen la función que generará la señal desfasada respecto de y:	h =1sin(2%pi220t+%pi);
Reproduzcan la función y + h:	playsnd(y+h)

¿Qué escuchan? ¿Cómo justifican el fenómeno generado?

Actividad 2

Volviendo a la matemática, para visualizar lo que se acaba de escuchar, pueden pedirles a sus alumnos que representen en GeoGebra las funciones y, z y h, y las sumas y + z e y + h, para observar cuál es el gráfico de la señal resultante en cada caso.

Para tener en cuenta (algunos problemas que nos suceden a los docentes cuando armamos las actividades y que es mejor que se las transmitamos a nuestros alumnos):

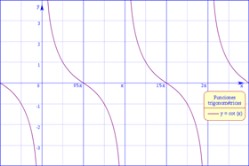
Si en GeoGebra se grafica la función y sin variar los límites de los ejes x e y (sin cambiar la escala), se observará un gráfico como el de la derecha. Es probable que recién al ver el gráfico, los alumnos tomen conciencia del efecto que se produce al ingresar una frecuencia tan alta (recuerden que en y la frecuencia es f = 220).

Para ver la curva que forma “la mancha negra”, pueden hacer clic en el fondo, o sobre los ejes, con el botón derecho del mouse, y entrar a Vista gráfica.

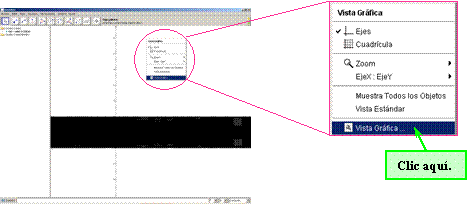
Se despliega otra ventana en la que se puede ajustar la escala ingresando los límites de ambos ejes:

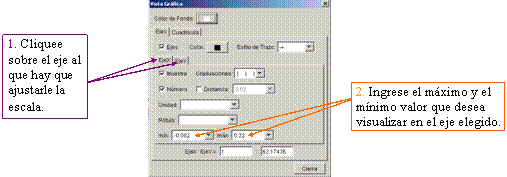
Otra situación que podría ocurrirles es que sus alumnos prueben más batidos, ingresando funciones en las que las variaciones entre las frecuencias fuesen más grandes; los mejores efectos sonoros se obtienen cuando la diferencia entre las frecuencias es pequeña, pero si es demasiado chica, es más difícil ver el efecto gráfico (para visualizarlo correctamente, hay que volver a cambiar los límites del eje x).
Si tienen alumnos inquietos y curiosos, alguno podría preguntar cómo se escucha la función f(x) = sen(x). En este caso, alcanzará con hacerles hallar la frecuencia. Recuerden que el hombre solo escucha sonidos cuyas frecuencias están entre 20 y 20.000 Hz (en el mejor de los casos).

Para finalizar, pueden pedirles a sus alumnos que elaboren un informe con las conclusiones obtenidas.

Enlaces de interés y utilidad para el trabajo

Conceptos básicos sobre el sonido