Funciones trigonométricas, parte 1
 |
Autores: Ana Verónica Veltri y Martín Miguel Pérez
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Funciones trigonométricas
Nivel: Secundario, ciclo orientado (escuelas técnicas)
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se abordarán los siguientes temas: relación entre los gráficos de las funciones seno, coseno y tangente, e interpretación gráfica de los parámetros que intervienen en la fórmula de una función del tipo 
También se analizará el modelo matemático asociado –entre otras cosas– a la generación de sonidos; una interesante aplicación de las funciones trigonométricas que encontrarán en “Funciones trigonométricas, parte II”.
Para poder realizar estas actividades, es necesario que los alumnos conozcan al menos las nociones básicas de trigonometría y ángulos expresados en radianes.
En esta secuencia se trabajará con el programa GeoGebra.
Objetivos de las actividades
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Objetivos pedagógicos
Actividad 1
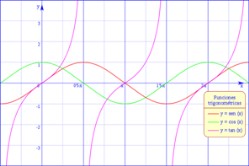
Esta actividad es para comparar los gráficos de la función tangente con los del seno y el coseno, a través del análisis de la identidad.
1) Utilizando el programa GeoGebra, representen las funciones seno y coseno. Para representar la primera, deben ingresar sin(x) en el campo de entrada. También pueden renombrarlas y colorearlas para identificarlas a simple vista.
2) Comparen los gráficos de ambas funciones y vean que, cuando una de las dos se anula, la otra tiene un máximo o un mínimo.
3) Comparen los valores de ambas funciones para cada valor de x. Gráficamente, es como comparar las ordenadas de los puntos que tienen las mismas abscisas en los dos gráficos.
4) Para eso, utilizando la herramienta 
, coloquen un punto que se desplace sobre el gráfico del seno para obtener sus coordenadas. Como es el primer punto que se ingresa, por defecto el programa lo nombrará A.
5) Hay varias formas de obtener un punto sobre el gráfico del coseno con la misma coordenada xque A. Una forma rápida es ingresando: B = (x(A)), cos(x(A)).
6) Ahora es el momento de usar la identidad. En el campo de entrada, ingresen un nuevo punto con la sentencia: C = (x(A), y(A) / y(B)).
7) Como B y C dependen de A, al desplazar A (recuerde que solo pueden hacerlo sobre el gráfico del seno), también se desplazarán B y C.
8) El punto C, en su desplazamiento, recorre el gráfico de la tangente. Para visualizarlo fácilmente, activen el rastro del punto, haciendo un clic sobre C con el botón derecho del mouse y tildando la opción Activar rastro.
9) Pueden elegir para C un color no muy oscuro, de manera que no oculte las otras funciones. (Recuerden que con Control + F pueden borrar el rastro, pero no desactivarlo).
En esta instancia pueden notar, entre otras cosas, que:
- los ceros de la función seno coinciden con los ceros de la tangente;
- si el seno es igual al coseno, la tangente vale 1;
- a medida que el coseno se aproxima a un cero, la tangente tiende a infinito.
Por último, vean que el trazo dejado por C coincide con el gráfico de la tangente ingresando en el campo de entrada: Tan(x). Al apretar Enter, se visualizará el gráfico de la tangente sobre el rastro de C.
Actividad 2
Con esta actividad se pueden analizar las variaciones del gráfico de la función al modificar sus parámetros.
1) Pídanles a sus alumnos que representen la función en el programa GeoGebra, pero para no perder los parámetros, primero deben definirse, con la posibilidad de modificarse fácilmente.
Para eso, se debe hacer clic en la herramienta 
, y luego, clic en cualquier lugar de la pantalla. Aparecerá la siguiente ventana:
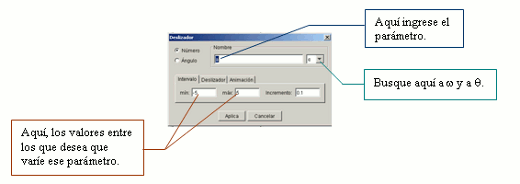
Se puede nombrar A al primer parámetro que ingresa; para los otros dos, se trabaja de manera similar.
2) Ya se puede ingresar la función, escribiendo en el campo de entrada:
(recuerden respetar los espacios).
Pueden colorearla ingresando al cuadro de propiedades.
Al utilizar cada deslizador, el gráfico se va modificando. Puede ingresarse también la función seno (prescindiendo de los parámetros) para que pueda realizarse la comparación.
Además, si lo desean, también pueden pedirles a sus alumnos que ingresen la función coseno y que varíen los parámetros de f, hasta que ambas funciones coincidan (observe que 
dará un valor aproximado, por ejemplo: 1,6, en vez de 
). ¿Hay ás de una forma de hacer que ambos gráficos coincidan?