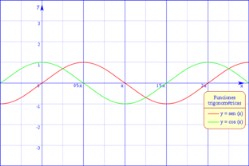
Funciones seno y coseno
 |
Autores: Laura Spivak y Pablo J. Kaczor
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Seno y coseno
Nivel: Secundario, ciclo orientado (escuelas técnicas)
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia les proponemos que construyan e interpreten los gráficos de las funciones seno y coseno.
Se abordarán los siguientes temas: interpretación de los segmentos que representan el seno y el coseno de un ángulo en la circunferencia trigonométrica; interpretación y construcción de los gráficos de las funciones seno y coseno, y utilización del programa GeoGebra. Es necesario que, previamente, se haya trabajado con la secuencia “Grados y radianes” antes de abordar estas actividades (ver secuencia “grados y radianes”).
Objetivo de las actividades
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Objetivos pedagógicos
Actividad 1:
1) Trabajen reunidos de a dos o tres alumnos. En primer lugar, preparen una circunferencia trigonométrica. Para hacerlo, abran el programa GeoGebra y sigan los pasos realizados en la actividad 2 de la secuencia “Grados y Radianes”; pero en lugar de marcar una semirrecta, marquen el punto P sobre el eje x (ver secuencia “grados y radianes”).
a) Hagan que el segmento OA’ no muestre su rótulo y que el punto A no sea visible.
b) Guarden el archivo de GeoGebra con el nombre “Circunferencia trigonométrica”.
Ya tienen todo listo para empezar a trabajar con el seno de a.
2) ¿Qué segmento lo representa?
Para visualizar el segmento, en el campo de entrada, ingresen las coordenadas de un punto del eje x, cuya abscisa sea la del punto A’. Llámenlo A’_x.
Ahora hagan que α sea un ángulo de primer cuadrante y tracen el segmento que representa el seno de α; píntenlo con un color con el que se destaque y llámenlo sen α. Hagan que muestre su rótulo.
3) Inserten un texto que muestre el valor del sen α. Para ello, copien lo siguiente (pueden copiar y pegar):
“sen α =” + (y(A’))
Pinten el texto con el mismo color que el segmento trazado.
4) Muevan el punto P; observen qué sucede y respondan estas preguntas en el procesador de textos:
a) ¿En qué cuadrantes sen α toma valores positivos?
b) ¿Para qué valores de α se cumple que sen α = 1?
c) ¿Y sen α = –1?
d) ¿Y sen α = 0?
5) En el campo de entrada, ingresen un punto S cuya abscisa sea la del punto P, y su ordenada, la del punto A’. Píntenlo de algún color que se destaque y activen su rastro.
6) Muevan el punto P: ¿qué ocurre?, ¿qué curva se va dibujando?
7) Para comprobarlo, en el campo de entrada, ingresen: f(x) = sin(x). Vuelvan a mover el punto P y respondan:
a) ¿Por qué para que se vaya trazando esa curva al mover el punto P, las coordenadas del punto S son las que se indicaron?
b) Observen el gráfico que queda marcado y verifiquen si respondieron correctamente las preguntas a, b, c y d, del punto 4.
c) ¿Cuál es el máximo de la función? ¿Para qué valores del dominio lo alcanza?
d) ¿Cuál es el mínimo de la función? ¿Para qué valores del dominio lo alcanza?
e) ¿Cuáles son las raíces de la función?
f) ¿Es una función periódica? ¿Cuál es el período?
8) Hagan que f(x) no sea visible.
9) Guarden el archivo de GeoGebra y el del procesador de textos con el nombre “Función seno”.
Actividad 2:
1) Reunidos de a dos o tres alumnos, van a trabajar de manera similar a la actividad 1, pero ahora con la función coseno.
2) Abran el archivo de GeoGebra que guardaron con el nombre “Función seno” y cámbienle el nombre por “Función coseno”.
3) Desactiven el rastro del punto S.
4) Hagan que α sea un ángulo de primer cuadrante y tracen el segmento que representa el coseno de α; píntenlo de un color que se destaque (distinto al que usaron para el seno), y aumenten su grosor y pónganle como nombre cos α.
5) Inserten un texto que muestre el valor de cos α. Para ello, copien esto:
“cos α =” + (x(A’)).
6) Pinten el texto con el mismo color que el segmento que trazaron.
7) En el campo de entrada, ingresen un punto C cuya abscisa sea la del punto P, y su ordenada, la abscisa del punto A’. Píntenlo de algún color que se destaque y que sea diferente al de S, y activen su rastro.
8) Tracen el segmento CP y hagan que tenga el mismo color y grosor que el segmento cos α.
9) Muevan el punto P: ¿qué ocurre?, ¿qué función queda representada?
10) Para comprobarlo, en el campo de entrada, ingresen: g(x) = cos(x). Vuelvan a mover el punto P y respondan la siguiente pregunta en el procesador de textos:
a) ¿Por qué para que se vaya trazando esa curva al mover el punto P, las coordenadas del punto C son las que se indicaron?
11) Observen el gráfico que queda marcado y respondan estas otras preguntas:
b) ¿En qué cuadrantes cos α toma valores positivos?
c) ¿Para qué valores de α se cumple que cos α = 1?
d) ¿Y cos α = –1?
e) ¿Cuáles son las raíces de la función?
f) ¿Cuál es el máximo de la función? ¿Para qué valores del dominio lo alcanza?
g) ¿Cuál es el mínimo de la función? ¿Para qué valores del dominio lo alcanza?
h) ¿Cuál es el período de la función?
12) Hagan que g(x) no sea visible.
13) Activen el rastro del punto S, muevan el punto P y respondan:
i) ¿Qué pueden observar? ¿Cómo son las curvas?
j) ¿Para qué valores del dominio sucede simultáneamente que sen α = 0 y cos α = 1? ¿Y que sen α = 1 y cos α = 0?
k) Adrián afirma que cos α = sen (α + π/2). ¿Es cierto? ¿Cómo se dan cuenta?
l) Para comprobarlo, en el campo de entrada, ingresen: h(x) = sin (x + π/2). Muevan el punto P y observen.
¿Podrían enunciar con sus palabras lo que pudieron observar?
- Guarden el archivo de GeoGebra y el del procesador de textos con el nombre “Función coseno”.
Enlaces de interés y de utilidad para el trabajo
Aplicaciones de Matemática y Física con GeoGebra
¿Para qué sirve la trigonometría?
Funciones trigonométricas. GeoGebra
Geometría dinámica. Función seno
Geometría dinámica. Función coseno