Función homográfica
 |
Autores: Ana Verónica Veltri y Martín Miguel Pérez
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Función homográfica
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se estudiará la función homográfica y su introducción a partir de una aplicación geométrica usual (la relación entre la base y la altura de rectángulos de la misma área), y descontextualizar el modelo y analizarlo.
Para resolver las actividades, es necesario que los alumnos manejen el concepto de función y que sepan analizar funciones más sencillas. Se utilizarán el programa GeoGebra y el programa de hojas de cálculo.
Objetivos de las actividades
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Actividad 1
1) Piensen en una situación hipotética en la que disponen de una determinada cantidad de revestimiento acrílico y quieren saber cuáles son las dimensiones máximas de una pared que pueda cubrirse con el material disponible (por ejemplo, si la cantidad de revestimiento alcanza para cubrir una superficie de 10 m2 de área).
2) Armen una tabla utilizando el programa de hoja de cálculos, disponible en sus equipos portátiles. En la primera columna, ingresen distintas posibilidades para la base, y en la segunda, la fórmula que devuelve la altura para cada base ingresada. Es importante que, como se está trabajando con una situación concreta, empleen valores posibles.
3) A partir de esta situación, pueden concluir que la relación entre la base y la altura de la pared para cubrir mantienen una relación de proporcionalidad inversa, y que la constante de proporcionalidad es el área.
Actividad 2
1) Ahora piensen en un rectángulo cualquiera. También pueden representar la función que da la altura del rectángulo, conocida la base (para un área determinada). Luego pueden variar el área y ver qué efectos se producen en el gráfico. Para realizar esta actividad, trabajen con un archivo del programa GeoGebra, que pueden descargar haciendo clic aquí.
2)
En el archivo encontrarán dos deslizadores: uno, para elegir el área
que se desplaza “a mano” (también pueden utilizar el deslizador y
manejarlo a través de las flechas del teclado), y el otro, para mostrar
la variación de la base. Este se desplaza automáticamente haciendo clic
en 
, que se encuentra en el extremo inferior izquierdo de la pantalla.
Para la base, se consideraron los valores 0,01 y 16 como mínimo y máximo del deslizador (respectivamente); si lo desean, cámbienlos desde sus propiedades.
Indicaciones para el docente
Para trabajar con el archivo, indíquenles a sus alumnos un área determinada y pídanles que activen la animación (hagan clic en ): las coordenadas del punto P
indican los valores correspondientes a las dimensiones de los distintos
rectángulos con esa área. Si activan el rastro, verán el gráfico que
forma dicho punto.
Pueden repetir el procedimiento variando el área. Tengan en cuenta que antes de cambiar el valor del área, hay que desactivar el rastro (y volverlo a activar justo antes de iniciar la animación).
Después de emplear varias áreas, el archivo se verá así:
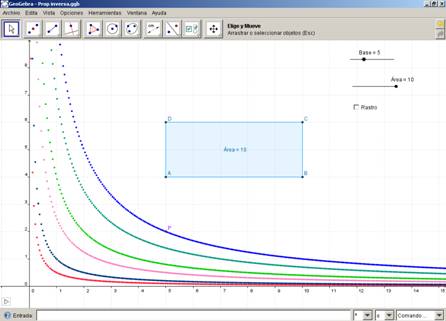
Recuerden que el rastro se borra apretando Control + F.
También pueden pedirles a sus alumnos que escriban las fórmulas de las funciones representadas.
Para verificar que la fórmula es correcta, ingrésenla en el campo de entrada del mismo archivo de GeoGebra. Al apretar Enter, el gráfico obtenido debe coincidir con el rastro dejado por P.
Nota: la fórmula puede ingresarse directamente escribiendo en el campo de entrada, por ejemplo: f(x) = 10 / x, (o g(x) =…, o h(x) = …). Pero si al ingresarla emplean algún parámetro usado, tal vez les aparezca algún error (o algo extraño); en tal caso, intenten ingresarla así: función [10/x, 0,01, 16].
Esta actividad también puede servir para introducir la noción de asíntota (y la de límite).
Actividad 3
En esta instancia se puede descontextualizar completamente el modelo empleado y analizarlo en sí mismo.
A partir de una función de la forma 
, pueden analizar el dominio y la imagen, y su variación según el valor del parámetro k (para esto es de gran ayuda que observen lo realizado en la actividad anterior y ampliarlo para el caso k < 0). Si mencionaron las asíntotas, pueden hacerles notar que ellas siguen siendo las mismas, aun variando k.
Además, se puede trabajar con funciones homográficas descentradas del origen y ver la relación entre el gráfico y la fórmula.
También
pueden utilizar el programa GeoGebra y pedirles a sus alumnos que, en
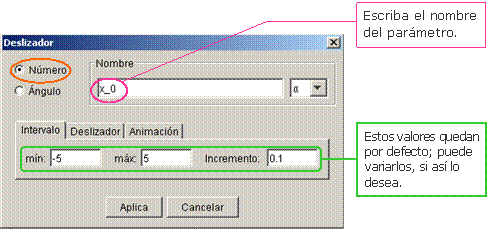
un archivo nuevo, ingresen tres deslizadores numéricos haciendo clic en
. Los deslizadores corresponden a:
- k: factor (igual que en la función mencionada con anterioridad);
- x_0: dará la abscisa del centro de la hipérbola;
- y_0: corresponde con la ordenada del centro.
A continuación, ingresen la función en el campo de entrada, respetando los parámetros anteriores:
f(x) = k / (x – x_0) + y_0.
Al apretar Enter, aparecerá el gráfico correspondiente con la función, cuyos parámetros son los valores numéricos que se observan en los deslizadores.
Así los alumnos podrán ver cuáles son los desplazamientos que se producen en el gráfico, según los parámetros que varíen mediante los deslizadores. También podrán identificar las asíntotas en cada caso.
Pueden preguntarles qué ocurre si k = 0, o en qué caso el modelo corresponde a una proporcionalidad inversa.
Para finalizar, pídanles a sus alumnos que investiguen en qué otras áreas se emplean las funciones de proporcionalidad inversa (por ejemplo, algunas relaciones que se desprenden de la Ley de Ohm o de la Ley de Boyle Mariotte), para que re-contextualicen los contenidos aprendidos y elaboren (en grupos de dos o tres personas) una actividad de aplicación.