Derivadas
 |
Autor: Sebastián Vera, Javier Peña, Daniel Brizuela y Rodrigo Weber
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Derivadas por definición
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección caracterizaremos aquellas funciones cuyo gráfico es suave. Esto es, aquellas funciones cuyo gráfico no tenga picos o vértices (ejemplo de una función cuyo grafico tiene un pico en x=0 es la función módulo). Desde un punto de vista geométrico, ser suave en un punto significa que es posible graficar una recta tangente al gráfico de la función en dicho punto. Las funciones suaves son las que llamaremos derivables. Para comprender mejor este concepto, observaremos los videos presentados a continuación.
1) Derivadas
Objetivos de las actividades
Introducir en el concepto de derivada usando su definición.
Interpretar gráficamente la definición de derivada.
Determinar gráficamente en qué puntos no es derivable una función.
Relacionar e interpretar situaciones problemáticas asociadas a derivadas en un punto para comprender el uso de la herramienta matemática.
Integrar y relacionar continuidad de una función con derivadas en un punto.
Objetivos pedagógicos
Actividad 1
Para las funciones dadas:
i. f(x)= 2x-7 en (2;-3) ii. f(x)= x2 en (2;4) iii. f(x)=(x+2)1/2 en (2;2)
a) Utilicen la definición de derivada para hallar el valor de la pendiente de las rectas tangentes a las gráficas de cada curva en los puntos que se indican.
b) Hallen la ecuación de la recta tangente.
c) Grafiquen las curvas y las rectas tangentes. Pueden graficarlas, desde su equipo portátil, utilizando el programa generador de gráficos (Winplot), que tienen instalados en sus equipos portátiles, para poder representar las funciones en el eje de coordenadas.
d) Estimen el valor de las funciones en x=2+1/13 utilizando la ecuación de la recta tangente.
Actividad 2
En cada gráfico:
a) Determinen los puntos donde la función no es derivable. Expliquen por qué.
b) Determinen los intervalos donde f’(x)>0.
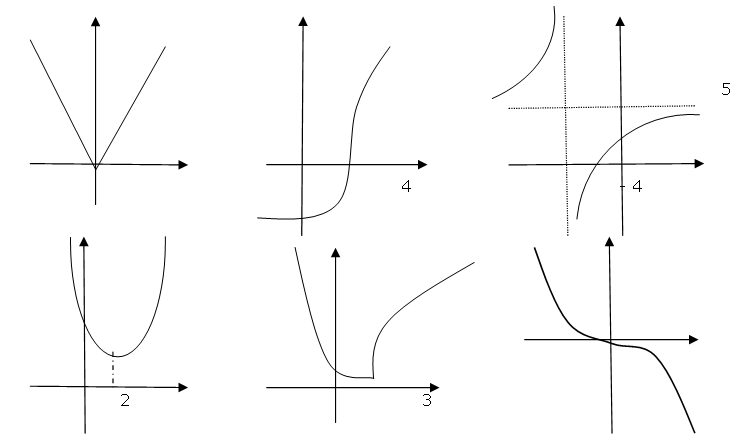
Actividad de cierre
Debido a unas pésimas condiciones ambientales, una colonia de un millón de bacterias no comienza su reproducción hasta pasados dos meses. La función que representa la población de la colonia al variar el tiempo (expresado en meses) viene dada por:
![]()
Se les pide que:
a) verifiquen que la población es función continua del tiempo;
b) grafiquen la función utilizando el programa generador de gráficos (Winplot), que tienen instalado en sus equipos portátiles, y verifiquen el resultado del punto anterior;
c) calculen la tasa de variación media de la población en los intervalos [0,2] y [0,4].
d) calculen la tasa de variación instantánea en t=4.