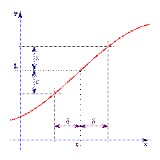
Concepto e interpretación gráfica del límite de una función en un punto
 |
Autor: Rodrigo Weber, Sebastián Vera, Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Límite de una función
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Objetivos de las actividades
Comprender el concepto de limite de una función, ya sea analítica o gráficamente.
Resolver ejercicios que involucren el límite de una función.
Objetivos pedagógicos
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
La idea de límite de una función está relacionada con los valores que toma la función en lugares cercanos a un punto que haya despertado nuestro interés. De ahora en más cuando se diga “límite de una función en algún punto”, se deberá entender que interesa saber el comportamiento de la misma en una zona muy cercana al punto.
Actividad 1
1) Supongamos que tenemos esta función: 
describe la posición, en kilómetros, de un móvil en función del tiempo transcurrido (x = tiempo en horas). Y queremos saber:
a) ¿En qué posición estaba el móvil a las dos horas de haber partido? Para hacerlo, utilicen algunos de los programas graficadores (Winplot o Geogebra) instalados en para graficar la función.
b) Ahora la pregunta es: ¿a qué posición se acerca el móvil si el tiempo transcurrido tiende a ser de 2 horas? Para analizar esta pregunta, tomen valores cercanos a x=2. Elaboren una tabla de valores (x; f(x)). Para hacerla, pueden utilizar el procesador de textos y para realizar los cálculos utilicen la calculadora científica instalada en sus equipos portátiles.
c)¿Hay algún cambio con respecto a lo que se preguntó en el ítem a? Discutan y analicen las respuestas de otros compañeros.
Actividad 2
Ahora supongamos que tenemos la siguiente función 
y nos preguntamos:
1) ¿Qué le sucede a la función cuando x=2? ¿Existe f(2)? Si es así, ¿cuánto vale?
2) Grafiquen la función. Para ello, utilicen uno de los graficadores disponibles en sus equipos portátiles.
3) ¿A qué valor fijo del eje y se acercan los valores de f cuando los valores de x tienden a x=2? Para analizar esta pregunta, tomen valores cercanos a x=2. Elaboren una tabla de valores (x; f(x)). Para hacerla, pueden utilizar el procesador de textos y para realizar los cálculos utilicen la calculadora científica instalada en sus equipos portátiles.
4) Discutan con sus compañeros y el docente lo analizado en el ítem anterior. Luego saquen conclusiones sobre lo realizado en esta actividad.
Actividad de cierre
Para profundizar, analicen y discutan junto con el docente el concepto y la definición de límite de una función. Desarrollen una demostración para exponer en clase. Para ello, recomendamos que observen el video Límites: explicación con ejemplos y, si es necesario, busquen en Internet otros links que les sean útiles para desarrollar este tema.