Análisis de funciones polinómicas
 |
Autores: Sebastián Vera, Rodrigo Weber y Javier Peña
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Análisis gráfico y analítico de una función polinómica
Nivel: Secundario, ciclo orientado
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección trabajaremos con funciones polinómicas, con correspondencia entre gráficos y fórmula de la función polinómica. En las actividades los alumnos podrán analizar la correspondencia entre el gráfico de una función polinómica y su fórmula, identificando sus raíces y sus intervalos de crecimiento, decrecimiento, positividad y negatividad.
Objetivos de las actividades.
Que los alumnos:
- Analicen la correspondencia entre gráficos y fórmula de una función polinómica.
- Interpreten gráficos e identifiquen raíces, conjuntos de positividad y negatividad de una función.
- Apliquen temas vistos en unidades anteriores (operaciones entre polinomios y factorización) para analizar diferentes funciones polinómicas.
Actividad 1
1) En grupos de dos o tres alumnos, analicen la siguiente situación y respondan las preguntas:
En un laboratorio se realizó un estudio para una colonia de microorganismos. Durante los días que duró la investigación no se proporcionaron alimentos y se estableció que la cantidad m (en millones) de microorganismos variaba en función del tiempo t (en días) transcurridos desde que se originó el estudio, según la siguiente expresión:
m(t) = -t2 + 3t +4
a) ¿Cuál o cuáles de los siguientes gráficos describe la variación de la cantidad de microorganismos en función del tiempo (desde que se comenzó con el estudio). Justifiquen su elección y expliquen por qué descartan los otros.
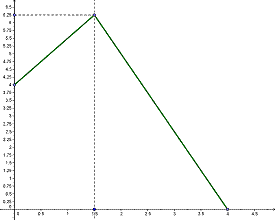
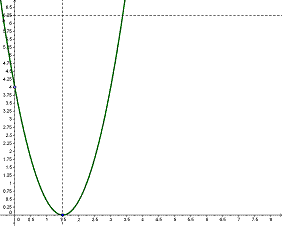
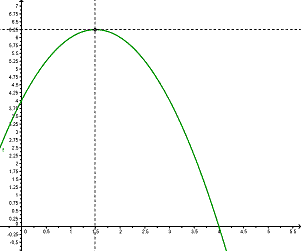
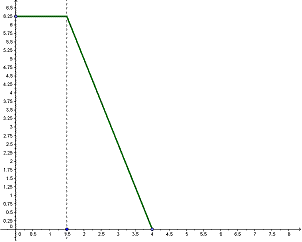
b) ¿Con qué cantidad de microorganismos comenzó el experimento?
c) ¿Desaparecen todos los microorganismos en algún momento? Si es así, ¿cuándo?
d) ¿En algún instante de tiempo la cantidad de microorganismos es la misma que la cantidad con la que se inició el experimento? En el caso afirmativo, calculen ese tiempo.
e) ¿Pueden estimar en qué momento la cantidad de microorganismos es máxima?
f) ¿En qué período se estudia el proceso? ¿En qué intervalo se representa la cantidad de microorganismos en este experimento?
g) ¿Cuál es el dominio y la imagen de la función m(t)? Distingan entre el dominio natural, es decir el dominio matemático de la fórmula, y el dominio propio de la situación analizada. ¿Es el mismo en cada caso?
h) Para repasar y profundizar estos temas ingresen en los siguientes links:
Dominio e imagen de una función
i) Realicen un resumen de lo analizado en el ítem h) explicando brevemente las siguientes cuestiones:
- ¿Qué es una función polinómica? ¿Como es su expresión o fórmula matemática?
- ¿Qué son los ceros o raíces de una función? ¿Cuál es su interpretación gráfica?
- ¿Qué son los intervalos de crecimiento y decrecimiento? ¿Y los de positividad y negatividad? ¿Cuál es su interpretación grafica?
Actividad 2
1) El siguiente gráfico corresponde a una función polinómica de grado 3.
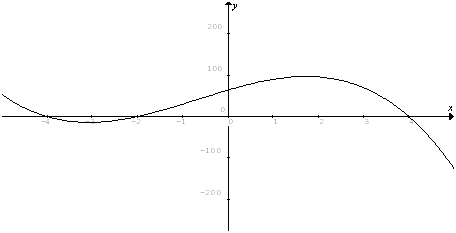
a) Indiquen cuánto valen las imágenes para los siguientes valores: x = -4, x = -2 y x = 4. ¿Cómo se denominan estos valores?
b) Teniendo en cuenta que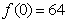 
,
hallen el valor del coeficiente principal de la función cúbica
graficada y escriban su fórmula. ¿Es la única fórmula posible? Comparen
los resultados con sus demás compañeros.
2) Escriban el conjunto de ceros (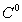
) y los conjuntos de positividad y negatividad (
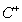y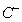 
) de una función de grado 3, que cumpla con las siguientes condiciones en cada caso:
, 
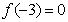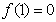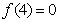
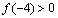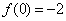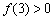y 
, 
, 
y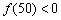 
a) Con los datos anteriores, realicen un gráfico aproximado de la función en cada caso y comparen los gráficos hechos por sus demás compañeros. ¿Son los mismos? Discutan junto con su docente.
Actividad de cierre
1) Dada la siguiente función polinómica:
F(x) = (x + 2) . (x + 5) . (x - 3)
a) Indiquen cuáles son sus raíces. ¿Podría tener esta función otras raíces diferentes de las indicadas? Justifiquen su respuesta.
b) ¿Puede la función F(x) tomar un valor positivo para un valor x en el intervalo (-2, 3), y un valor negativo para otro x en el mismo intervalo? ¿Por qué?
c) Utilicen el programa GeoGebra o Winplot, instalados en sus equipos portátiles, para graficar la función F(x).
2) Marquen la o las opciones correctas en cada caso, y justifiquen su decisión.
La función f(x) = x3 + x2 verifica que:
a) La única raíz real es x = 0
b) La gráfica interseca al eje horizontal en x = -1
c) La gráfica interseca al eje vertical en y = -1
d) Existen dos números reales que son raíces de la función