Triángulos rectángulos y relación pitagórica.
 |
Autores: Mercedes Sens Hourcade, Rodrigo Weber y Sebastián Vera
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Analizar las relaciones entre lados de triángulos rectángulos. Y Comprender el teorema de Pitágoras para aplicarlo en diferentes situaciones.
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia trabajaremos la relación que existe entre los lados de un triángulo rectángulo, más conocida como Teorema de Pitágoras.
Objetivo de las actividades
Que los alumnos:
Verifiquen si se cumple el Teorema de Pitágoras en triángulos rectángulos.
Construyan ternas pitagóricas a partir de una terna dada.
Apliquen el Teorema de Pitágoras a situaciones problemáticas concretas.
Objetivos pedagógicos
Actividad 1
Los lados de un triángulo rectángulo guardan una relación muy especial.
1) Visiten los siguientes links para conocer cuál es esta relación y cómo se llama.
Teorema de Pitágoras, en Wikipedia
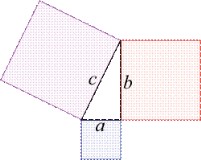
2) En los siguientes triángulos, indiquen cuáles son los catetos y cuál es la hipotenusa:

3) Utilicen el programa Geogebra para verificar que se cumple el teorema de Pitágoras, para eso construyan tres triángulos utilizando como ángulo recto la intersección de los ejes y completen la siguiente tabla colocando en cada celda las longitudes de los catetos y la longitud de la hipotenusa.
Cateto A |
Cateto B |
Hipotenusa |
|---|---|---|
Luego verifiquen que se cumple la siguiente igualdad: H2=A2+B2
4) Junto con sus compañeros y el docente debatan las siguientes cuestiones:
a) ¿Si multiplico la terna (H, A y B) por algún número natural se sigue cumpliendo el teorema?
b) ¿Se cumple el Teorema de Pitágoras en triángulos que no son rectángulos?
c) Actualmente, se sabe que existen más de trescientas demostraciones del Teorema de Pitágoras. Visiten los siguientes links, para conocer una de estas demostraciones:
Teorema de Pitágoras, en YouTube
5) En base a lo visto en el punto anterior, expliquen, con sus palabras, en qué consisten las demostraciones desarrolladas en cada link.
Actividad 2
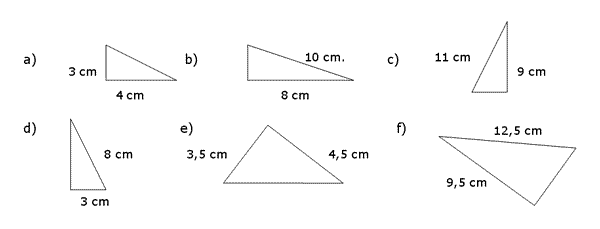
1) Utilizando el Teorema de Pitágoras, calculen la medida del lado que falta en cada uno de los siguientes triángulos rectángulos. Utilicen la calculadora científica, instalada en sus equipos portátiles, para realizar todos los cálculos necesarios.
2) Resuelvan las siguientes situaciones y justifiquen sus respuestas:
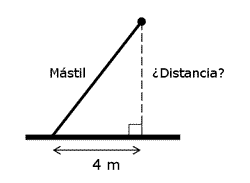
a) Una tormenta inclina el mástil de la bandera de una escuela, que tiene 6 metros de longitud (ver figura). ¿Qué distancia hay entre la punta del mástil y el pie de la altura?
b) Si se apoya una escalera, de 2 m de longitud, contra una pared, de modo tal que el pie de la escalera se encuentra a de 1, 5 m de distancia de la pared. ¿A qué altura se encuentra el otro extremo de la escalera?
c) Si se quiere dividir un terreno rectangular por su diagonal, y el terreno tiene un largo de 50 m y un ancho de 20 m, hallen la longitud del alambre necesario para realizar la división.
d) Un joven se encuentra perdido en el bosque, después de varias horas de caminata encuentra a un guarda parque, este le explica que existen dos caminos posibles para llegar a su campamento:
- Camino 1 (dos tramos) = caminar en línea recta unos 6000 metros, luego girar 90º a su derecha y caminar algunos kilómetros hasta el campamento.
- Camino 2 (un tramo) = desviarse unos 25º hacia su derecha y caminar 9 kms en línea recta hasta toparse con el campamento.
El joven estudia las dos posibilidades y con la ayuda de su brújula dibuja el siguiente mapa:
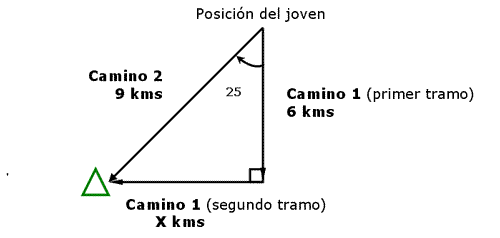
¿Cual será el camino más corto para llegar al campamento? ¿Por qué?
Actividad de cierre.
1) Investiguen en Internet o en otras fuentes sobre las siguientes cuestiones:
a) ¿Quiénes fueron los primeros en la historia en aplicar el Teorema de Pitágoras? ¿Cómo y para qué lo utilizaban?
b) ¿Quién fue Pitágoras? Escribir una breve reseña biográfica sobre él. Para ello utilicen el procesador de textos, instalado en sus equipos portátiles.
Enlaces de interés y utilidad para el trabajo
Explicación del Teorema de Pitágoras
Teorema de Pitágoras, en YouTube
Demostraciones gráficas del Teorema de Pitágoras