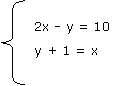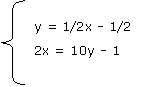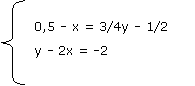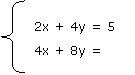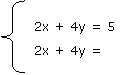Resolución de sistemas de ecuaciones lineales con dos incógnitas
 |
Autores: Javier Peña, Sebastián Vera y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Ecuaciones lineales con dos incógnitas
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Introducción a las actividades
En esta secuencia se abordará cómo interpretar, analizar y resolver sistemas de ecuaciones lineales de primer grado con dos incógnitas. Los alumnos podrán comprender de qué manera se puede plantear un sistema de ecuaciones de primer grado en una situación concreta y analizarán las soluciones de diferentes sistemas de ecuaciones lineales con dos incógnitas.
Objetivos de las actividades
Analizar y comparar diferentes sistemas de ecuaciones lineales con dos incógnitas.
Plantear y resolver sistemas de ecuaciones con dos incógnitas.
Objetivos pedagógicos
Actividad 1
Sergio trabaja en una granja. Por la mañana tuvo que contar la cantidad de gallinas y conejos que hay, pero se llevó una sorpresa al observar que estos animales no estaban en su lugar. Por suerte se encontró con su amigo Luis, que también trabaja en la granja y había contado a los animales el día anterior.
Sergio: –Hola, Luis. ¿Cuántos animales contaste ayer?
Luis: –Yo conté en total, entre gallinas y conejos, 121 cabezas y 342 patas.
Sergio: –Entonces, ¿cuántas gallinas y conejos hay en la granja?
1) Analizando los datos que obtuvo Luis, respondan las siguientes consignas:
a) Traten de hallar la cantidad de conejos y gallinas. Para ello utilicen la calculadora científica instalada en sus equipos portátiles.
b) ¿Cuántas incógnitas hay en el problema? Identifiquen cada una con una letra diferente.
c) ¿Podrían resolver esta situación planteando una ecuación de primer grado?
d) ¿Cuántas ecuaciones deberían plantear para resolver este problema?
e) Propongan las ecuaciones necesarias para encontrar la cantidad de gallinas y conejos e intenten resolverlas. Comparen sus resultados con los demás compañeros. Pueden observar el siguiente video como ayuda para planear las ecuaciones.
e) Si Luis hubiese contado un total de 341 patas, ¿qué habría pasado con la cantidad de gallinas y conejos? Debátanlo entre todos junto con el docente.
Actividad 2
1) Encuentren tres soluciones distintas para cada ecuación.
a) 2x + 1 = 11y
b) -4x + 3y = 10
c) 1/2x - y +1 = 0
2) Dados los siguientes sistemas de ecuaciones:
a) |
b) |
c) |
Para cada sistema, verifiquen en qué casos los valores de x = 1 e y = 0 son soluciones de:
la primera ecuación;
la segunda ecuación;
del sistema de ecuaciones.
3) Resuelvan los sistemas del ítem anterior en los cuales no se hayan verificado los valores de x e y propuestos.
En todos los casos utilicen la calculadora científica instalada en sus equipos portátiles para hacer todos los cálculos necesarios.
Actividad de cierre
1) Analicen las soluciones de los siguientes sistemas de ecuaciones. Utilicen la calculadora científica instalada en sus equipos portátiles para realizar todos sus cálculos.
a) |
b) |
2) ¿Pudieron resolverlos? Discutan junto con el docente sobre las soluciones que puede tener un sistema de ecuaciones y traten de clasificarlos según lo debatido.
Enlaces de interés y utilidad para el trabajo
Sistema lineal de dos ecuaciones con dos incógnitas
Sistemas de ecuaciones lineales con dos incógnitas en forma gráfica
Matemáticas finitas resumen del tema: sistemas de ecuaciones lineales y matrices