Reales. Ubicación de números irracionales en la recta numérica
 |
Autor: Gustavo Romero
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Números irracionales
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
Esta secuencia estudiaremos los siguientes temas: el análisis de propiedades del orden en reales y la introducción al trabajo con algunas expresiones irracionales en un contexto geométrico.
Antes de abordar estas actividades, es conveniente que los alumnos manejen adecuadamente conceptos básicos de geometría, en particular el teorema de Pitágoras.
Por otro lado, es necesario que los alumnos tengan una idea previa de la diferencia entre el valor exacto y el valor aproximado de un número para darle sentido a la búsqueda por medio de herramientas geométricas del lugar en la recta de los números que queremos ubicar.
Para el desarrollo de esta actividad utilizaremos como soporte geométrico y algebraico el programa Geogebra.
Objetivos de las actividades
Introducir a los alumnos al uso de herramientas geométricas y algebraicas sencillas para la construcción de figuras con la computadora como soporte, a partir de la ubicación de números irracionales en la recta numérica.
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Objetivos pedagógicos
Actividad 1
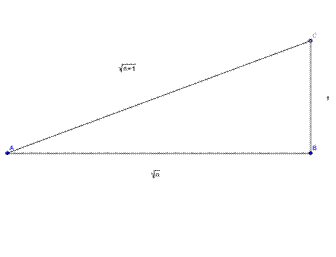
Como trabajo preliminar, proponemos trabajar la relación entre las medidas de un triángulo rectángulo cuyos catetos miden 1 y ![]() , con
, con ![]() .
.
La propuesta es llegar a la generalización con los chicos, que la terna (1,![]() ,
, ![]() )
es una terna pitagórica. La demostración algebraica es sencilla, y se
la puede dejar a los alumnos. Lo más importante es que puedan
verbalizar la propiedad ya que la van a usar en la actividad.
)
es una terna pitagórica. La demostración algebraica es sencilla, y se
la puede dejar a los alumnos. Lo más importante es que puedan
verbalizar la propiedad ya que la van a usar en la actividad.
![]()
![]() ,
, ![]()
Demostrada
esta propiedad, podemos avanzar en la propuesta de ubicar, utilizando
Geogebra, algunos números irracionales sencillos, como por ejemplo ![]() .
.
Para la representación, en la ventana de Geogebra, es más cómodo quitar el eje de ordenadas, de manera tal que quede solo el eje de abscisas como recta numérica. Para esto, haciendo clic derecho sobre el plano, en el menú “propiedades”, tomaremos la solapa “eje y”, y desactivaremos su muestra.
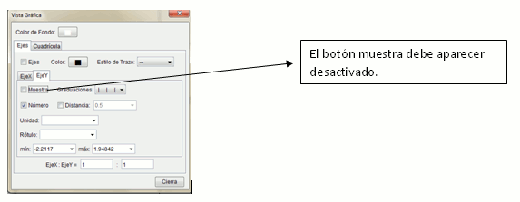
La intención es construir, sobre la recta, triángulos rectángulos con un vértice en cero de manera tal que la medida de su hipotenusa sea la misma que el número que queremos representar.
Para las
sucesivas construcciones usaremos una recta paralela a la recta
numérica, a distancia 1, que podemos trazar ingresando en la barra de
entradas la ecuación ![]() .
.
En el caso de![]() , el triángulo rectángulo buscado es aquel que tiene por catetos 1 y 1.
, el triángulo rectángulo buscado es aquel que tiene por catetos 1 y 1.
1) Con la opción “marcar punto” -![]() -, marcamos el 0 y el 1 en la recta.
-, marcamos el 0 y el 1 en la recta.
2) A continuación trazamos por 1 una perpendicular a la recta –para hacerlo presionamos el botón ![]() y elegimos el punto y la recta-
y elegimos el punto y la recta-
3)
El tercer vértice del triángulo rectángulo es la intersección entre la
recta y=1 y la perpendicular que acabamos de trazar –que podemos hallar
con el programa usando el botón “intersección entre objetos” ![]() .
.
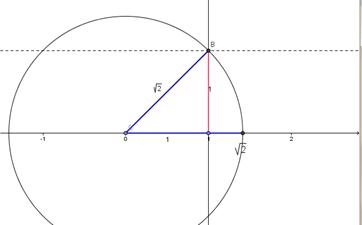
De
esta forma nos queda determinado en la gráfica el triángulo buscado, de
manera que lo único que nos queda por hacer es transportar la medida de
la hipotenusa (que en este ejemplo mide ![]() )
sobre la recta. Para hacerlo, trazamos la circunferencia con centro en
0 y usando como radio la hipotenusa del triángulo construido.
)
sobre la recta. Para hacerlo, trazamos la circunferencia con centro en
0 y usando como radio la hipotenusa del triángulo construido.
Propuestas para debatir con los alumnos
- Para representar
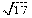 , ¿habrá que repetir el proceso 16 veces?
, ¿habrá que repetir el proceso 16 veces? - ¿Cómo representarías
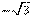 a partir del trabajo ya hecho?
a partir del trabajo ya hecho? - ¿Y para representar
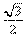 ? (Sugerencia: se puede usar la herramienta “mediatriz”
? (Sugerencia: se puede usar la herramienta “mediatriz”  ).
). - ¿Se puede representar cualquier número irracional con éste método?, ¿Qué alcances tiene?
- Ubicá en la recta el número de oro
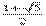 . Explicá paso por paso cómo lo hallaste.
. Explicá paso por paso cómo lo hallaste.