Proporcionalidad
 |
Autores: Damián Gibellieri, Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Razones y proporciones
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Impulsar el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Incitar la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia trabajaremos el concepto de razón y proporción entre diferentes magnitudes. En las actividades los alumnos podrán comprender qué es una razón y qué es una proporción entre diferentes cantidades. Además trabajarán con la relación que existe entre magnitudes directamente proporcionales, al analizar diferentes situaciones.
Objetivos de las actividades
Que los alumnos:
Apliquen propiedades para el cálculo de extremos y medios.
Reconozcan magnitudes directamente proporcionales y realicen sus modelos gráficos.
Reconozcan la constante de proporcionalidad.
Fomenten la investigación matemática como medio de aprendizaje.
Actividad 1
Cuando llevamos a revelar o imprimir una fotografía, nos ofrecen diferentes alternativas de tamaño, pero la imagen sigue siendo la misma, es decir, tiene siempre las mismas proporciones, aunque varíe su tamaño.
1) Visiten los siguientes links para comprender cuándo dos cantidades o magnitudes son proporcionales:
2) A partir de lo leído en el ítem anterior, analicen las siguientes situaciones:
a) Tenemos una fotografía de 10 x 15 cm y necesitamos ampliarla, pero es necesario que en la ampliación no pierda su forma original. En el negocio me ofrecen distintos tamaños: 13 x 18 cm, 15 x 21 cm y 20 x 30 cm. ¿Cuál me recomiendan ustedes? ¿Por qué?
b) Una fotografía de 13 x 18 cm se amplía a razón de 5/2. ¿Cuál es el tamaño de la fotografía ampliada?
Actividad 2
1)Encuentren la razón que mantenga la proporcionalidad entre las siguientes cantidades:
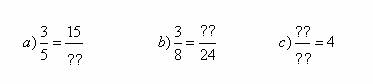
b) Hallen el valor de la constante k que permita comprobar la siguiente proporcionalidad:
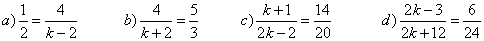
Actividad 3
1) Analicen y resuelvan las siguientes situaciones:
a) Un cuaderno tiene 41 hojas, y otro cuaderno, 97. ¿Cuántas hojas más debería tener el cuaderno de 97 para que su razón sea 1/3?
b) La razón de las áreas de dos triángulos es 3/5. El área del triángulo más grande es 55 cm2. ¿Cuál es el área del triángulo más chico?
c) El perímetro de un cuadrado se relaciona en forma directamente proporcional con la longitud de sus lados. Utilizando el programa de hoja de cálculo, instalado en sus equipos portátiles, construyan una tabla similar a la que se muestra abajo, y completen los espacios en blanco. Para ello, relacionen el perímetro de un cuadrado según la longitud de sus lados:
Longitud del lado (en cm) |
5 |
2 |
15 |
||
|---|---|---|---|---|---|
Perímetro (en cm) |
24 |
28 |
d) Utilicen los datos de la tabla anterior y el programa GeoGebra, instalado en sus equipos portátiles, para graficar los diferentes cuadrados. ¿Los cuadrados dibujados son proporcionales entre sí? Justifiquen su respuesta.
Actividad de cierre
1) Realicen esta actividad reunidos en grupos de dos o tres alumnos.
Sabiendo que una planta recicladota de basura recicla 33 kg de abono por cada 1.000 kg de basura, resuelvan las siguientes consignas:
a) Construyan una tabla similar a la que se muestra abajo y calculen la cantidad de abono que se obtiene según la cantidad de basura reciclada. Utilicen la calculadora científica, instalada en sus equipos portátiles, para realizar todos los cálculos necesarios.
Kg. de basura |
Kg. de abono |
|---|---|
1.000 |
33 |
2.000 |
|
2.700 |
|
3.507 |
|
4.326 |
|
6.743 |
|
7.654 |
|
8.090 |
|
12.541 |
b) ¿Es proporcional la relación entre la cantidad de basura y la cantidad de abono que se obtiene? Si es así, ¿cuál sería la constante de proporcionalidad?
c) Utilicen los datos de la tabla anterior y el programa GeoGebra para realizar un gráfico que muestre la cantidad de abono obtenido, en función de la cantidad de kilos de basura.
d) Encuentran alguna relación entre la constante de proporcionalidad y la inclinación de la recta graficada en el ítem anterior.
e) Hallen alguna ecuación que represente la cantidad de kilos de abono en función de la cantidad de kilos de basura.
f) Si tenemos 12.431,87 kilos de abono, ¿cuántos kilogramos de basura se reciclaron? (Ayuda: utilicen la ecuación del ítem anterior).
g) ¿Con 300 kilos de basura, podremos reciclar algo? Justifiquen su respuesta.