Polígonos y propiedades
 |
Autores: Damián Gibellieri y Javier Peña
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Polígonos y propiedades
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección el alumno podrá trabajar las propiedades de los ángulos interiores y exteriores de un polígono, y sacar conclusiones sobre la relación entre sus diagonales y el valor de sus ángulos. También será capaz de hallar la relación entre estos últimos y los polígonos en general, utilizando como herramienta de geometría el programa Geogebra.
Objetivos de las actividades
Que los alumnos:
Reconozcan las distintas características de los polígonos.
Reconozcanlos polígonos regulares y no regulares al conocer sus propiedades.
Interpreten y resuelvan las situaciones problemáticas.
Actividad 1
En el mundo físico hay muchos ejemplos de formas geométricas, es por esto que se piensa que la naturaleza nos proporcionó las primeras nociones de geometría. Por ejemplo, podemos ver hexágonos en la estructura de un panal de abejas o diferentes figuras, como pentágonos o triángulos, entre los pétalos de muchas flores. Con el paso del tiempo, el hombre ha utilizado estos polígonos para crear muchos objetos y estructuras útiles para la sociedad.
1) Armen una lista de cinco objetos o estructuras creadas por el hombre que estén diseñadas o construidas con base en polígonos.Para recordar qué es un polígono y cómo se clasifica, ingresen en los siguientes links:
Polígonos regulares y círculos
a) Escriban un resumen de lo analizado en cada link.
b) Utilicen el programa Geogebra, instalado en sus equipos, para realizar las siguientes actividades:
- Dibujen un polígono regular con 4, 6, 8, 10 y 12 lados, y clasifíquenlo.
- Dibujen diferentes figuras -que no sean regulares- de 3, 4, 5, 6, 7 y 8 lados, y marquen los ángulos interiores y exteriores de cada una de ellas.
2) Dibujen un polígono de 9 lados y tracen sus diagonales desde un solo vértice, por ejemplo, a (el programa automáticamente marca con una letra cada vértice del polígono dibujado).
a) ¿Cuántas diagonales pudieron marcar en este polígono? ¿Cuántos triángulos hay en el polígono?
b) Ahora hagan lo mismo con todos sus vértices (b, c, d, etc.) y cuenten el total de sus diagonales. ¿En cuántos triángulos quedó dividido el polígono? ¿Cuánto vale la suma de sus ángulos interiores y exteriores? (Para verificar sus cálculos, pueden marcar los ángulos utilizando Geogebra, y luego calculen la suma de los ángulos con la calculadora que tienen instalada en sus equipos).
c) ¿Cuánto valdrá la suma de los ángulos exteriores de un polígono de 10 lados? ¿Y si tuviera 11 lados?
d) Intenten encontrar una expresión general o fórmula que les permita calcular la suma de los ángulos exteriores de un polígono de n lados.
Actividad 2
1) Utilicen el programa Geogebra para realizar las siguientes actividades:
a) Dibujen figuras similares a estas, midan y sumen cada uno sus ángulos interiores.
 |
 |
 |
 |
 |
 |
 |
|
 |
b) ¿En qué casos es posible aplicar la propiedad de los ángulos interiores y exteriores trabajada en la Actividad 1? ¿Cuáles de ellos la pueden utilizar? Justifiquen su respuesta y saquen una conclusión.
2) ¿Se podrá dividir un hexágono regular para formar:
a) 4 triángulos isósceles;
b) 6 triángulos equiláteros;
c) 2 trapecios isósceles;
d) 2 trapecios escálenos;
e) 3 rombos?
Actividad de cierre
1) El polígono regular estrellado (no confundamos con un polígono estrella) tiene sus vértices consecutivos unidos entre sí, que lo recorren en forma continua. Veamos cómo podemos construir uno de estos polígonos utilizando el programa Geogebra. Construiremos un octógono estrellado formado por dos cuadrados.
- Dibujen un cuadrado.
- Tracen las diagonales en cada vértice. Esto lo pueden hacer con el ícono Segmento formado por dos puntos.
- Marquen el centro del cuadrado. Utilicen el comando Intersección de dos objetos; en este caso será la intersección de las diagonales.
- Ahora hay que rotar el cuadrado a 45º. Para esto van a tener que prestar atención.
Veamos:
Primero vayan al ícono Rotar objeto en torno a un punto, y luego sigan las instrucciones que se marcan. El ángulo que van a rotar es de 45°.
Háganlo girar a partir del centro que habían marcado anteriormente.
Por último unan cada vértice entre sí y tendrán su octógono estrellado. Los lados de los cuadrados nos marcan prácticamente todas las diagonales. Hay que terminarlas de marcar.
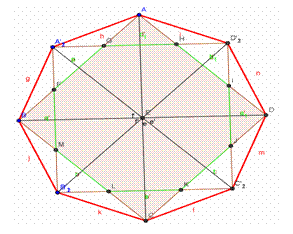
- ¿Se animan a construir un dodecaedro?
Ayuda: primero van a tener que girar el cuadrado a 30°, luego seleccionarlo otra vez y, cambiando el sentido (a horario), girarlo nuevamente con un ángulo de 30°.
