Polígonos regulares
 |
Autores: Claudia
Ugrin, Javier Peña, Rodrigo Weber y Sebastián Vera Responsable
disciplinar: Sebastián Vera Área
disciplinar: Matemática Temática:
Polígonos Nivel:
Secundario, ciclo básico Secuencia didáctica
elaborada por Educ.ar |
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección el alumno se familiarizará con los elementos del polígono regular. Aprenderá a graficar polígonos utilizando regla y compás, y usando programas de geometría.
Objetivos de las actividades
Que los alumnos:
Identifiquen polígonos y aprendan su denominación.
Conozcan los elementos de los polígonos.
Reconozcan los distintos ángulos de un polígono regular.
Grafiquen polígonos regulares con regla y compás o software.
Actividad 1
Un polígono es una figura plana cerrada delimitada por segmentos. A estos segmentos se les llama lados.
Un polígono es regular cuando todos sus ángulos y lados son iguales. En caso contrario el polígono es irregular.
Según el número de lados, los polígonos se pueden clasificar en:
|
Nombre |
n.º de lados |
Nombre |
n.º de lados |
|---|---|---|---|
|
Triángulo |
3 |
Octógono |
8 |
|
Cuadrilátero |
4 |
Eneágono |
9 |
|
Pentágono |
5 |
Decágono |
10 |
|
Hexágono |
6 |
Dodecágono |
12 |
|
Eptágono |
7 |
Icoságono |
20 |
1) Junto con el docente analicen los videos que aparecen en los siguientes links:
2) Observen la figura. Nombren los segmentos y ángulos que aparecen marcados en el polígono.
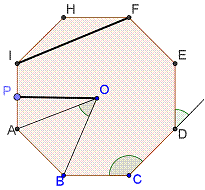
Segmento: IF, OP, AO, HI, BO, FE,
Ángulos: AOB, BCD, EDW
Por ejemplo: El segmento BO es el radio del polígono.
a) ¿Cómo se llama el polígono de la figura?
3) Con Geogebra, dibujen un eneágono. Marquen la mediatriz de cada uno de sus lados.
a) ¿Se cruzan? ¿En dónde?
b) ¿Cómo se llama el segmento que se formó desde el punto medio del lado al punto en común?
c) Ahora dibujen una circunferencia con tres de los puntos que las mediatrices forman con los lados.
4) Con Geogebra, dibujen otro eneágono. Marquen los segmentos que se forman con cada vértice y el centro.
a) ¿Cómo se llama ese segmento?
b) Ahora dibujen una circunferencia con tres vértices del polígono.
5) Respondan las siguientes preguntas:
a) ¿Cuál es el centro de la circunferencia? ¿Y el del polígono?
b) ¿En qué circunferencia esta inscripto el polígono?
c) Enuncien la propiedad que relaciona al polígono con esa circunferencia.
Actividad 2
1) A partir de una circunferencia se pueden construir diferentes polígonos regulares utilizando solo regla y compás. Junto con el docente visiten el siguiente link para comprender cómo se dibuja un polígono regular usando regla y compás:
a) En base a lo analizado dibujen en sus carpetas, utilizando regla y compás, los siguientes polígonos regulares.Indiquen el ángulo central de cada polígono.
Triángulo equilátero
Cuadrado
Hexágono
Octógono
b) Redacten los pasos necesarios para construir cada polígono anterior.
1) También se pueden construir polígonos regulares conociendo el valor del ángulo central.
Con Geogebra, dibujen ángulos consecutivos de 120º. Luego dibujen una circunferencia cuyo centro sea el vértice y que contenga a los puntos determinados por los ángulos. Tracen los segmentos que forman los puntos consecutivos.
¿Qué figura se formó?
a) Repitan el procedimiento con ángulos consecutivos de amplitud 60º. ¿Qué polígono regular se formó?
2) ¿Es posible dibujar polígonos regulares a partir del valor de un ángulo interior?
a) Con el programa Geogebra, tracen un ángulo de 120º. Luego dibujen la circunferencia que forman esos tres puntos (ninguno de ellos es centro). Sigan dibujando ángulos inscriptos con la misma amplitud. Unan los segmentos que forman los puntos consecutivos. Nombren el polígono obtenido.
b) Repitan el procedimiento para un ángulo de 108º
Actividad de cierre
En grupos de dos o tres alumnos investiguen en internet o en otras fuentes:

a) ¿Que son los teselados?
b) ¿Que civilizaciones antiguas lo utilizaban?
c) ¿Cual era su propósito?
d) Construyan su propio teselado, e indiquen los polígonos utilizados.