Números racionales
 |
Autores: Mercedes Sens Hourcade, Sebastián Vera, Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Introducción a los números racionales, fracciones orden y densidad
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección nos dedicaremos a estudiar los números racionales (forma fraccionaria), los ubicaremos en la recta numérica y estudiaremos la densidad de este conjunto.
Objetivos de las actividades
Reconocer números racionales.
Ubicar los números racionales en la recta numérica.
Analizar la densidad de los números racionales.
Objetivos pedagógicos
Actividad 1
1) Completen la siguiente tabla colocando los valores que representan la misma cantidad que las fracciones de la primera columna.
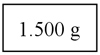
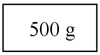
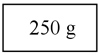
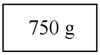
 |
|
 |
|
 |
|
 |
2) Utilizando el programa Geogebra, ubiquen en la recta numérica las fracciones que están expresadas en el ítem anterior. Recuerden que la unidad está expresada en kg.
3) A partir del ítem anterior, ordenen de menor a mayor las cantidades representadas.
Actividad 2
Juan debe encontrar el número que se encuentra justo en la mitad de los que propone Ana. Completen cada fila del siguiente cuadro según corresponda:
|
Ana |
Juan |
|---|---|
|
Entre 0 y 2 |
1 |
|
Entre 0 y 1 |
½ |
|
Entre 0 y ½ |
|
|
Entre 0 y |
|
|
Entre 0 y |
|
|
Entre 0 y |
a) ¿En qué momento se termina? ¿Cuántos números podemos encontrar? ¿Ocurre lo mismo con los números enteros?
2) Utilizando el programa Geogebra, ubiquen en la recta numérica los números que propone Juan.
Actividad de cierre
A partir de la siguiente recta numérica:

1) Hallen el valor de a.
2) Encuentren un número (b) que esté entre a y 3.
3) Encuentren un número (c) que esté entre 2 y b.