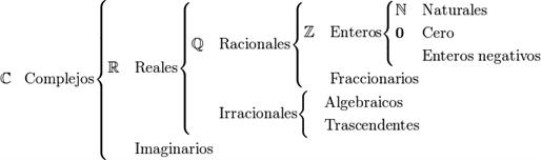
Números irracionales
 |
Autores: Sebastián Vera, Javier Peña, Daniel Brizuela.
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Noción de número irracional. Algunos números especiales √2 (raíz cuadrada de dos) y φ (fi) (número de oro)
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades:
A través de estas actividades los alumnos comenzarán a familiarizarse con el concepto de número irracional. En la primera actividad deberán calcular la diagonal de un cuadrado de lado 1cm. Mediante el uso de la calculadora y el programa Geogebra podrán observar que √2 en su expresión decimal no tiene una cifra periódica, con lo cual no es posible escribir este numero como una fracción, por lo tanto √2 no pertenece a los números racionales. Además si el docente lo considera necesario, se muestran algunos links para que los alumnos puedan analizar la demostración de porque √2 no se puede escribir como un cociente entre dos números enteros. Por ultimo se proponen otras actividades para que los alumnos conozcan otro numero irracional como el número de oro φ (fi).
Objetivos de las actividades
Analizar situaciones y resolver problemas para discriminar y caracterizar los números racionales e irracionales.
Interpretar la noción de número irracional √2 y número de oro φ (fi) mediante el estudio de su expresión decimal.
Conocer diferentes aplicaciones del número de oro φ (fi).
Objetivos pedagógicos
Actividad 1
Entre los siglos VI y V a. C., existió en Grecia la Escuela Pitagórica, llamada así en honor a su fundador, Pitágoras de Samos. Para los pitagóricos, toda la naturaleza estaba determinada por números enteros o fracciones de enteros (lo que nosotros conocemos como números racionales). Hasta que un día, un estudiante de esta escuela llamado Hipaso descubrió y demostró la existencia de otra clase de números: los números inconmensurables o irracionales.
Probablemente, Hipaso se encontró con los números irracionales resolviendo problemas muy parecidos a estos:
1) ¿Cuánto vale la diagonal de un cuadrado de 1 cm de lado? Para realizar este cálculo, pueden utilizar la calculadora que tienen en sus equipos portátiles. Comparen el resultado obtenido con los de sus compañeros.
a) ¿Cuántos decimales (números después de la coma) tiene el valor calculado?
2) Ahora, grafiquen el cuadrado de 1 cm de lado en el programa graficador (Geogebra), que está instalado en sus equipos portátiles.
a) Usen el comando de distancia/longitud que se encuentra en la barra de herramientas para medir la longitud de la diagonal del cuadrado. ¿Tiene el mismo valor que la que calcularon ustedes?
b) Usen el comando redondeo que se encuentra en el menú opciones para obtener más números decimales. ¿Qué sucede con estos?
3) Junto con sus compañeros y el docente, discutan la siguiente cuestión:
a) ¿El valor de la diagonal puede ser un número racional? Si fuese así, ¿qué debería suceder?
4) Junto con el docente, analicen alguna de las demostraciones matemáticas que aparecen a continuación, donde se demuestra por qué √2 no puede ser un número racional.
Actividad 2
1) En grupos de dos o tres integrantes, dibujen pentágonos regulares con diferentes medidas. Para ello, utilicen el programa graficador (Geogebra), que se encuentra instalado en sus equipos portátiles.
2) En el programa de hojas de cálculo, instalado en sus equipos portátiles, armen una tabla como se muestra a continuación:
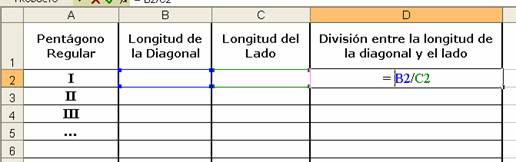
3) Para cada pentágono, midan la longitud de uno de los lados y la longitud de una de las diagonales. Coloquen estas medidas en la tabla anterior. Las celdas de la última columna deben tener un formato de diez decimales o más.
4) En cada pentágono dibujado, dividan la diagonal por el lado y escriban este resultado en la última columna. Pueden hacer este procedimiento escribiendo la fórmula que aparece en el cuadro (fila 2, columna D). Cópienla en las filas siguientes.
5) ¿Cuál fue el número que obtuvieron al dividir la diagonal por uno de sus lados? Comparen sus resultados con los demás grupos y discutan sobre el valor obtenido.
6) ¿Este valor será siempre el mismo para cualquier pentágono regular dibujado? ¿Puede ser un número racional?
Actividad de cierre
El número que se consigue al dividir la diagonal de un pentágono regular por cualquiera de sus lados recibe un nombre especial, ya que aparece tanto en Matemática como en el arte, en la arquitectura de edificios, en las Ciencias naturales y en muchas otras áreas. Vean el video que se encuentra en el siguiente link para saber más sobre este número.
1) Realicen un resumen de lo que vieron en el video.
2) ¿En qué situaciones aparece este número?
3) Si tienen acceso a Internet, investiguen algunas de las situaciones en las que aparece este valor, y expongan lo investigado frente a los demás grupos.
Enlaces de interés y utilidad para el trabajo
Historia de los números irracionales