Métodos analíticos y gráficos para la resolución de ecuaciones lineales con dos incógnitas
 |
Autores: Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Resolución de sistema de ecuaciones con dos incógnitas
Nivel:Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se trabajarán distintos métodos de resolución de sistemas de ecuaciones lineales de primer grado con dos incógnitas. Para ello los alumnos investigarán en páginas especializadas u otras fuentes métodos de resolución y, mediante el programa Geogebra, graficarán y verificarán la solución de los distintos sistemas planteados.
Objetivos de las actividades
Que los alumnos:
Analicen y compararen diferentes métodos de resolución de sistemas de ecuaciones lineales.
Grafiquen sistemas de ecuaciones lineales e interpreten las soluciones.
Clasifiquen las soluciones de un sistema de ecuaciones lineales.
Objetivos pedagógicos
Actividad 1
1) Analicen la siguiente situación:
Un coleccionista compró en una subasta 47 monedas, algunas de bronce y otras de plata. Las monedas de bronce le costaron $14 cada una y las de plata, $18 cada una. Si en total gastó $750, ¿cuántas monedas de bronce compró y cuántas de plata?
2) La situación anterior se puede resolver planteando un sistema de dos ecuaciones lineales, de primer grado, con dos incógnitas. Discutan junto con el docente las siguientes cuestiones:
a) Para esta situación, ¿cuáles serían las incógnitas? ¿Cómo quedarían planteadas las ecuaciones?
b) Planteen un sistema de dos ecuaciones con dos incógnitas y traten de resolverlo. Ingresen al siguiente link, en donde se explican algunos métodos para resolver este tipo de sistemas.
c) Expliquen brevemente en qué consiste cada método analizado en el ítem anterior.
d) Resuelvan el sistema planteado en el ítem b aplicando los métodos explicados anteriormente. Utilicen el programa Geogebra o Winplot para representar gráficamente cada ecuación y verifiquen la solución hallada.
e) Investiguen en Internet qué otros métodos existen para resolver este tipo de sistemas de ecuaciones, y discutan junto con su docente las ventajas y desventajas de cada método.
Actividad 2
1) El resultado de un sistema de ecuaciones es X = 1 e Y = -3. Determinen a cuál de los siguientes sistemas pertenece este resultado:
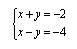
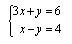
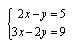
b) Utilicen el programa del Geogebra para graficar la recta de cada ecuación y verifiquen el resultado obtenido.
2) Escriban otro sistema de ecuaciones que tenga la misma solución del problema anterior. ¿Cuántos puede haber?
Actividad 3
1) Utilicen el programa Geogebra, instalado en sus equipos portátiles, para graficar cada uno de los siguientes sistemas de ecuaciones:
![]()
![]()
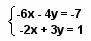
![]()
a) Para cada sistema de ecuaciones graficado, analicen cómo son las rectas entre sí.
b) Resuelvan los sistemas de ecuaciones anteriores aplicando alguno de los métodos analizados en la actividad 1.
c) Indiquen en qué casos pudieron encontrar una única solución, infinitas soluciones o ninguna solución.
d) ¿Cómo relacionarían cada solución hallada en el ítem d con los gráficos obtenidos en el ítem a? Clasifiquen las soluciones de cada sistema según las rectas obtenidas.
Actividad de cierre
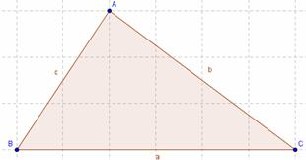
1) Hallen los lados del triángulo ABC con los datos que se indican a continuación:
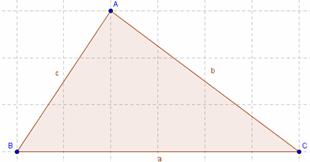
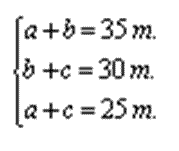
2) Los lados de un triángulo están determinados por las gráficas de las siguientes ecuaciones:
3x + y = 9
2x + 3y = -1
x - 2y = -4
a) Utilicen el programa Geogebra para graficar cada ecuación y encontrar los vértices del triángulo. ¿Cuáles son los puntos del vértice del triángulo formado?
b) Planteen un sistema de ecuaciones para cada par de lados, resuélvanlo y verifiquen las soluciones halladas en el ítem a.