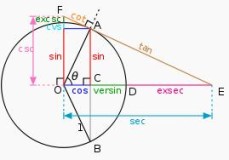
Función trigonométrica
 |
Autor: Rodrigo Weber
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Análisis de las funciones trigonométricas seno y coseno: variación de parámetros y construcción de gráficos
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia analizaremos las funciones trigonométricas seno y coseno. A lo largo de las actividades los alumnos tendrán que graficar estas funciones, analizar sus propiedades y observar sus corrimientos.
Objetivos de las actividades
Que los alumnos:
Analicen las funciones trigonométricas del seno y coseno, y estudien sus propiedades.
Relacionen e interpreten situaciones problemáticas mediante el uso de funciones trigonométricas.
Justifiquen y validen distintos conceptos analítica o gráficamente.
Actividad 1
Las funciones trigonométricas se usan para calcular situaciones en las que intervienen triángulos planos.
1) Ingresen en los siguientes links para trabajar con las razones trigonométricas seno y coseno. Y analicen cómo se representan las funciones trigonometriítas gráficamente trabajando con las imágenes interactivas que aparecen en los links.
2) Utilizando el programa Geogebra, grafiquen las funciones que se presentan a continuación. Para cada función indiquen imagen, dominio, amplitud, período, ceros de la función, máximos y mínimos en cada caso.
a) f(x) = 4sen (2x + 4p)
b) f(x) = cos (x + p)
c) f(x) = 5sen (-3x)
d) f(x) = 3cos (4x + p)
Actividad 2
1) Utilizando el programa Geogebra, grafiquen las funciones que se presentan a continuación. Luego, respondan si las afirmaciones que acompañan a cada función son verdaderas o falsas.
a) f(x) = sen x + 4, está desplazada 4 unidades con respecto al eje x.
b) f(x) = sen (x + 4p), está desplazada 4p hacia la derecha.
c) f(x) = sen (4x + p), tiene por ángulo de fase a p.
d) f(x) = cos(2x + 2p), tiene por ángulo de fase a 2p.
e) f(x) = cos(x - 6), está desplazada 6 unidades hacia abajo.
2) El péndulo de un reloj se mueve periódicamente y se separa 5 cm de la vertical. La ecuación que describe el movimiento es: S(t)= 5 sen 4 pt, esta ecuación representa la distancia de la pesa a la vertical, en función del tiempo (t).
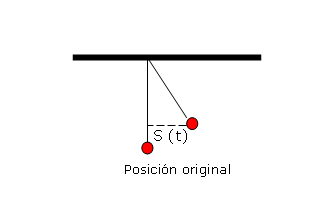
a) Representen gráficamente s(t).
b) Decidan a qué distancia de la vertical y de qué lado de ella (derecho o izquierdo) estará la pesa:
A los 4/3 seg.
A los 2 seg.
A los 17/8 seg.
c) ¿Qué distancia máxima alcanza el péndulo con respecto a la posición original?
d) ¿En qué instante el péndulo del reloj alcanza la distancia máxima?
e) Indiquen el período en el que se mueve el péndulo.
Actividad de cierre
1) En grupos de dos o tres alumnos, investiguen en Internet o en otras fuentes la biografía del matemático, astrónomo y geógrafo Ptolomeo.
2) Utilizando el procesador de textos instalado en sus equipos portátiles, redacten la biografía de este matemático. Hagan hincapié en cuáles fueron sus aportes en la matemática, la astronomía, la óptica y la música.