Expresiones algebraicas
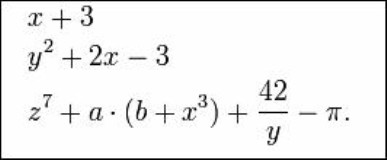 |
Autores: Sebastián Vera y Javier peña
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Expresiones algebraicas
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En este espacio se intentará interpretar expresiones matemáticas en las que números y letras se disponen de tal forma que permiten formular problemas y establecer leyes en el área. En las actividades, los alumnos trabajarán con el uso de letras para generalizar propiedades geométricas y numéricas. Además interpretarán fórmulas y expresiones algebraicas sencillas.
Objetivos de las actividades
Que los alumnos:
Reconozcan e interpreten fórmulas y expresiones algebraicas.
Utilicen las expresiones algebraicas para representar y generalizar propiedades geométricas y numéricas.
Realicen operaciones básicas con expresiones algebraicas.
Identifiquen y desarrollen algunos productos notables como el cuadrado de un binomio.
Actividad 1
1) En grupos de dos o tres alumnos realicen las siguientes actividades:
a) Utilicen el programa GeoGebra, instalado en sus equipos portátiles, para construir un rectángulo y un cuadrado. Calculen cuánto valen el perímetro y la superficie de las figuras construidas.
b) Comparen los resultados obtenidos por los demás grupos. ¿Todos obtuvieron el mismo resultado numérico?
c) Ahora utilicen letras a y b para nombrar los lados del rectángulo y la letra L para los lados del cuadrado. Expresen la superficie y el perímetro de cada figura usando las letras anteriores.
d) Comparen los resultados con el de los demás grupos. ¿Todos llegaron a la misma expresión?
e) Las expresiones obtenidas en el ítem anterior se denominan expresiones algebraicas, en estas expresiones intervienen números, letras y signos de operaciones, que se utilizan para generalizar diferentes propiedades y regularidades geométricas o numéricas. Para ampliar esta introducción, proponemos la lectura en el siguiente sitio:
Interpretación de fórmulas y expresiones algebraicas
Actividad 2
1) Expresen en forma algebraica el perímetro de las siguientes figuras:
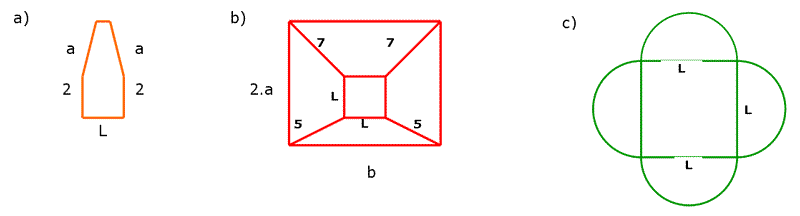
2) Para cada expresión algebraica obtenida en el ítem anterior, calculen el perímetro de cada figura reemplazando el valor de cada letra por los siguientes valores:
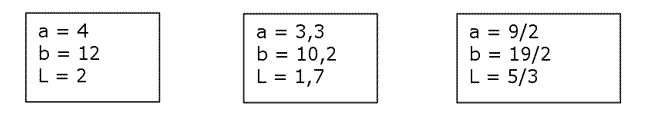
3) Si n es un número natural, ¿la expresión 3.n que número está representando? ¿Y 10.n?
4) Encuentren una expresión algebraica que les permita expresar:
a) Todos los números pares positivos.
b) Todos los múltiplos de 7.
c) Todos los números impares positivos.
d) Dos números naturales consecutivos.
e) Dos números pares, positivos, consecutivos.
f) Dos impares, positivos, consecutivos.
g) Tres impares, positivos, consecutivos.
Actividad de cierre
1) A partir del siguiente cuadrado de lados a + b, escriban las superficies para cada una de las 4 figuras que componen el cuadrado:
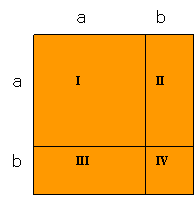
a) SI (Superficie del cuadrado I) =
b) SII (Superficie del rectángulo II) =
c) SIII (Superficie del rectángulo III) =
d) SIV (Superficie del cuadrado IV) =
2) Hallen la superficie total del cuadrado de lados a + b de dos formas diferentes:
a) Teniendo en cuenta el lado (a + b) del cuadrado,
b) Como sumas de las superficies halladas en el ítem 1) (SI + SII + SIII + SIV).
3) ¿Las superficies halladas en 2A) y B) son iguales? Justifiquen su respuesta.
4) Las dos expresiones algebraicas obtenidas en el ítem 3 son utilizadas frecuentemente en álgebra y reciben un nombre especial. Ingresen en el siguiente link para analizar este tipo de expresiones conocidas como productos o igualdades notables.
5) Relacionen cada expresión de la columna izquierda con la expresión de la columna derecha, de manera que resulten expresiones equivalentes.
a) (x + 3)2
b) X2 - 25
c) (x + 5) - (x - 5 + x2)
d) 2x . (x2 - 4)
i) 10 - x2
ii) 2x3 - 8x
iii) X2 + 9 + 6x
iv) (x + 5) . (x - 5)
Enlaces de interés y utilidad para el trabajo
Expresiones algebraicas (en catalán)