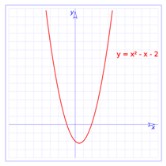
Estudio de la función cuadrática

	Autores: Javier Peña y Daniel Brizuela Responsable disciplinar: Sebastián Vera Área disciplinar: Matemática Temática: Formas canónicas, factorizadas y polinómicas Nivel: Secundario, ciclo básico Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

En esta secuencia, se estudiará la interpretación de la función cuadrática a través de sus distintas formas de expresión: formas polinómicas, formas factorizadas y formas canónicas. Para ello, se proponen diferentes actividades en las cuales los alumnos trabajarán con el pasaje de una expresión a otra, y analizarán en qué casos conviene utilizar cada expresión.

Objetivos de las actividades

Reconocer la función cuadrática, que se puede expresar de diferentes formas.

Expresar la función cuadrática en formas canónicas, factorizadas y polinómicas.

Representar gráficamente las distintas formas de la función cuadrática.

Objetivos pedagógicos

Actividad 1

En general, las funciones cuadráticas se expresan de la siguiente manera: y = ax² – bx – c, con a ≠ 0. Pero esta ecuación se puede expresar de distintas formas según el tipo de análisis que necesitemos realizar.

1) Para aprender cómo pasar de una forma de expresión a otra, visiten los siguientes links:

Análisis matemático - Diferentes ecuaciones para una sola parábola

Análisis de una función cuadrática

2) Luego de ver los videos, realicen un resumen con la información obtenida y respondan a las preguntas que se presentan a continuación:

a) Expresen de manera algebraica las distintas formas de escritura de una función cuadrática.

b) ¿Qué datos se obtienen en cada una de las expresiones anteriores?

c) ¿En qué casos conviene utilizar cada expresión?

Actividad 2

1) Analicen la siguiente situación y respondan a las preguntas:

Los meteorólogos de la provincia de San Luis determinaron que la temperatura media en el mes de agosto viene dada por la siguiente expresión:

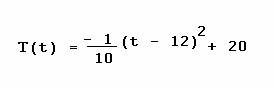
T es la temperatura media en grados centígrados (ºC) y t representa la hora del día.

a) Utilizando el programa graficador GeoGebra, representen la expresión anterior.

b) ¿Cuál fue la temperatura máxima en el mes de agosto? ¿A qué hora del día se registró?

c) ¿Qué temperatura se registró a las 3 de la tarde?

d) ¿Hubo temperatura por debajo de los 0 ºC? ¿A qué hora?

e) Expresen la ecuación dada por los meteorólogos, para la temperatura media de una forma diferente.

Actividad 3

1) Utilizando algunos de los programas graficadores (GeoGebra, Winplot o Graphmatica), grafiquen las funciones y completen los datos de cada columna:

Función	Raíces	Eje de simetría	Ordenada al origen	Vértice
y = x2 – 4x -5
y = -(x – 3)2 + 1
y = x (x + 4)
y = - (x – 1) (x -1)
y = - x2 + 2x -4

Actividad de cierre

1) Reunidos de a dos o de a tres alumnos, y utilizando el procesador de textos, disponible en sus equipos portátiles, construyan una tabla como la que se presenta a continuación:

Forma	Expresión de la función	Parámetro	Fórmulas para obtener raíces y vértices
Polinómicas o generales	y = ax2 + bx + c ; a¹0
Factorizadas			Xv = (X1 + X2)/2 ; Yv = f(Xv)
Canónicas		a; (Xv ; Yv)

Enlaces de interés y utilidad para el trabajo

Función cuadrática, en Wikipedia

Función cuadrática, en Fatela pre universitarios

Características de la función cuadrática

Función cuadrática: forma canónica