Ecuaciones de segundo grado

	Autores: Sebastián Vera, Javier Peña y Daniel Brizuela Responsable disciplinar: Sebastián Vera Temática: Resolución de ecuaciones de segundo grado Área disciplinar: Matemática Nivel: Secundario, ciclo básico Secuencia didáctica elaborada por Educ.ar

Propósitos generales

Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.

Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.

Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.

Introducción a las actividades

En esta secuencia, veremos cómo se plantean y cómo se resuelven problemas que involucran ecuaciones de segundo grado de manera explícita. Analizaremos sus procedimientos de solución, la existencia se sus propiedades y pertinencia de las soluciones obtenidas.

Objetivos de las actividades

Reconocer ecuaciones de segundo grado.

Resolver ecuaciones de segundo grado con una incógnita en forma numérica.

Aplicar los métodos de resolución anterior a problemas prácticos.

Objetivos pedagógicos

Actividad 1

En una ecuación existen cantidades desconocidas (incógnitas), que suelen designarse con las últimas letras del alfabeto: x, y, z; y cantidades conocidas (números fijos o coeficientes), que suelen designarse con las letras iniciales del alfabeto: a, b, c. Esta forma de representar las incógnitas y los coeficientes fue introducida por el matemático René Descartes en 1637.

Una ecuación de segundo grado tiene la siguiente forma:   .

Se dice que está completa, cuando se encuentran los siguientes términos: el término cuadrático (ax²), el término lineal (bx) y el término independiente (c). Para resolver este tipo de ecuaciones, es conveniente utilizar la siguiente expresión matemática o fórmula general de una ecuación cuadrática:

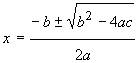
En el caso de que la ecuación de segundo grado se encuentre incompleta –es decir que no aparezca el término lineal (c) o el término independiente (bx)–, se deben utilizar algunas propiedades algebraicas que permitan resolver la ecuación, por ejemplo, extracción de factor común y completar cuadrados, entre otros.

1) Vean los siguientes videos:

Ecuaciones de segundo grado, fórmula general.

Ecuaciones de segundo grado por factorización.

2) Junto con el docente, analicen y discutan lo observado en los videos anteriores.

3) Dadas las siguientes ecuaciones cuadráticas, reconozcan los coeficientes a, b y c, en cada término de las ecuaciones:

a) 3x² - 5x + 2 = 0

b) 3x² - 5x = -2

c) 5x = -2 - x²

d) 0 = -2 + 3x²

e) 7 = 2x²

f) (x + 5).(x - 5) = o

g) x(x + 3) = 5x + 3

4) Para resolver las ecuaciones dadas anteriormente, utilicen la fórmula general de la ecuación cuadrática.

5) Analicen las soluciones que pueden tener las siguientes ecuaciones de segundo grado. Verifiquen todos los resultados obtenidos utilizando la calculadora científica instalada en sus equipos portátiles.

a) 4x² - 3x + 1 = 0

b) -4x² + 1 = 0

c) 3x² - 5x + 2 = 0

d) x² - x + 6 = 0

e) x² + 1 = 0

f) x² - 5x = 0

g) 2x² - 3x = 1

6) Redacten una conclusión sobre qué tipo de soluciones puede tener una ecuación de segundo grado.

Actividad 2

Planteen una ecuación cuadrática para resolver las siguientes situaciones. Verifiquen todos los resultados obtenidos utilizando la calculadora científica instalada en sus equipos portátiles.

Encuentren dos números cuya suma sea 28 y cuyo producto sea 187.

2) Encuentren tres números consecutivos cuyos cuadrados sumen 77.

3) Si un terreno rectangular tiene un perímetro de 88 m y un área de 475 m², ¿cuáles son sus dimensiones?

4) Si la edad de un padre es el cuadrado de la de su hijo, y dentro de 24 años,la edad del padre será el doble de la del hijo. ¿Cuántos años tiene ahora cada uno?

Actividad de cierre

Las ecuaciones de segundo grado no solamente son utilizadas en las matemáticas, también pueden ser utilizadas en física para resolver problemas de cinemática.

Por ejemplo: un proyectil parte con una velocidad inicial (v_i) de 20 m/s, luego de cierto tiempo (t), ha recorrido una distancia (d) de 150 m con una aceleración (a) de 2 m/s².

En grupos de 2 ó 3 compañeros, y con la ayuda de la calculadora científica instalada en sus equipos portátiles, realicen las siguientes actividades:

1) Calculen cuál será el tiempo (t) empleado por el proyectil, para recorrer esa distancia (d). Para ello, utilicen la siguiente fórmula:

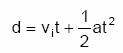
2) Calculen cuál sería el tiempo (t) empleado por el proyectil, si la distancia (d) recorrida fuera:

a) d = 100 metros

b) d = 10 metros

Enlaces de interés y utilidad para el trabajo

Ecuación de segundo grado, en Ejercicios de matemática

Ecuaciones de segundo grado, en Vadenúmeros

Webgrafía recomendada

Ecuación de segundo grado, en Wikipedia

Ecuaciones de segundo grado, en Thales

Ecuaciones de segundo grado, resolución e interpretación gráfica