Ecuación de la circunferencia
 |
Autores: Mercedes Sens Hourcade, Javier Peña y Rodrigo Weber
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Ecuación de la circunferencia
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia trabajaremos la ecuación de la circunferencia teniendo en cuenta su centro y su radio.
Objetivos de las actividades
Que los alumnos:
Reconozcan la ecuación de la circunferencia a partir del centro y del radio.
Analicen las variaciones de la ecuación de la circunferencia a medida que varía el radio.
Analicen las variaciones de la ecuación de la circunferencia a medida que varía el centro.
Reconozcan la circunferencia como lugar geométrico.
Actividad 1
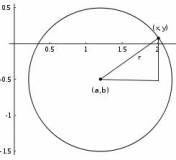
La circunferencia es una de las figuras geométricas más utilizadas en la historia de la humanidad. Si quisiéramos definirla matemáticamente, podríamos decir que es el conjunto de puntos que están en un mismo plano y que equidistan de otro punto llamado centro.
1) Ingresen al siguiente link para comprender el concepto de circunferencia y su ecuación general.
2) A partir de lo leído en el link anterior escriban la ecuación general de una circunferencia con centro en el origen de coordenadas. ¿En qué varía la ecuación si el centro es el punto (1; 2)?
3) Utilicen el programa Geogebra, instalado en sus equipos portátiles, para construir las siguientes circunferencias:
a) De centro (0; 0) y radio 1.
b) De centro (0; 0) y radio 2.
c) De centro (0; 0) y radio 3.
4) Luego completen la tabla que se presenta a continuación:
|
Centro |
Radio |
Ecuación |
|---|---|---|
|
(0; 0) |
1 |
|
|
(0; 0) |
2 |
|
|
(0; 0) |
3 |
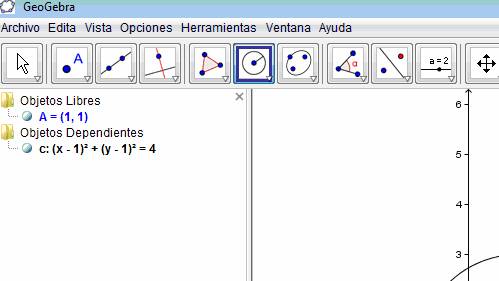
5) Escriban la ecuación de la circunferencia que figura a la izquierda de la pantalla, debajo del título objetos dependientes.
a) ¿Cómo será la ecuación de la circunferencia si el radio es 5?
Actividad 2
1) Utilizando el programa Geogebra, instalado en sus equipos portátiles, construyan las siguientes circunferencias y luego completen la tabla que figura abajo con la ecuación de la circunferencia que se muestra en el lado izquierdo de la pantalla del programa, debajo del título objetos dependientes.
|
Centro |
Radio |
Ecuación |
|---|---|---|
|
(0;3) |
2 |
|
|
(0;-3) |
2 |
|
|
(4;0) |
2 |
|
|
(-4;0) |
2 |
2) Ingresen al siguiente link y luego respondan:
a) ¿Cómo sería la ecuación de la circunferencia en el caso en que el centro esté ubicado en el punto (1; 2) y tenga radio 2?
b) Verifiquen la respuesta de la pregunta anterior utilizando el programa Geogebra.
Actividad de cierre
1) Utilizando el programa Geogebra, construyan dos circunferencias: una de centro (0; 0) y de radio 2, y la otra de centro (2; 0) y de radio 1.
a) Luego hallen el punto de intersección entre ambas. Para ello utilicen la opción el ícono punto 
, y hagan clic sobre la opción intersección de dos objetos 
.
Luego señalen con el puntero del mouse el punto de intersección de las
dos circunferencias. Al costado izquierdo de la página aparecerán las
coordenadas del punto de intersección buscado.
b) ¿A qué distancia está cada uno de los puntos del centro de ambas circunferencias? ¿Por qué?
Enlaces de interés y utilidad para el trabajo
Progresando en el conocimiento de la circunferencia