Continuidad
 |
Autores: Rodrigo Weber, Javier Peña y Daniel Brizuela
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Continuidad. Definición de continuidad. Discontinuidad evitable y esencial
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se trabajará con la definición de continuidad de una función desde el análisis geométrico y el analítico. A través de las herramientas de continuidad, los alumnos podrán plantear diferentes estrategias para hallar su solución y verificar la validez del resultado obtenido, ya sea gráfica o analíticamente.
Objetivos de las actividades
Que los alumnos:
Reconozcan y calculen funciones continuas y discontinuas analítica y gráficamente.
Estudien la continuidad de una función y clasifiquen sus discontinuidades.
Objetivos pedagógicos
Actividad 1
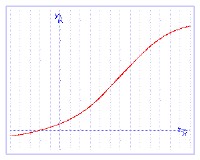
Las funciones continuas son aquellas cuyo gráfico puede realizarse con un trazo continuo, que “no pega saltos” ni tiene “agujeros”.
1) Visiten los siguientes links para conocer el concepto de función continua:
Continuidad y discontinuidad de una función
2) A partir de lo visto en los links, y en grupos de dos o tres alumnos, expliquen con sus palabras las siguientes cuestiones:
a) Gráficamente, ¿qué significa que una función sea continua en un punto? Den un ejemplo de una función que sea continua en x = 5 y otra que no lo sea en ese mismo punto. Para ello utilicen el programa Geogebra o el programa Winplot, ambos instalados en sus equipos portátiles.
b) ¿Qué casos de discontinuidad puede presentar una función? Den un ejemplo en cada caso. Utilicen el programa Geogebra para graficar la función propuesta en cada caso.
c) Desde el punto de vista analítico, ¿qué condiciones deben cumplirse para que una función sea continua en un punto?
Actividad 2
1) Indiquen si las siguientes afirmaciones son verdaderas o falsas. Justifiquen sus respuestas. En los casos en que la respuesta sea falsa, den un contraejemplo. Para responder utilicen el procesador de textos instalado en sus equipos portátiles y, en caso de tener que hacer algún gráfico, empleen el programa Geogebra, también instalado en sus equipos portátiles.
La existencia del límite es condición necesaria para que una función sea continua en un punto.
- La existencia del límite es condición necesaria para que una función sea continua en un punto.
- Para que una función presente una discontinuidad no evitable de salto finito debe verificarse obligatoriamente que no exista el límite de esa función en ese punto.
- La función
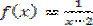es discontinua en x = 2. - Las funciones polinómicas de cualquier grado son siempre continuas para cualquier valor de x.
- Las funciones logarítmicas f(x) = log (ax + b) son siempre continuas para cualquier valor de x.
- Todas las funciones cuadráticas f(x)= ax 2 + bx + c son continuas para cualquier valor de x.
Actividad de cierre
1) Clasifiquen la discontinuidad de las funciones presentadas a continuación para los valores que se piden en cada caso. Utilicen el programa Geogebra o el programa Winplot, ambos instalados en sus equipos portátiles, para graficar cada función y tener una mayor apreciación del tipo de discontinuidad que presenta cada una.
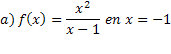
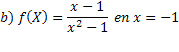
Enlaces de interés y utilidad para el trabajo
YouTube - Continuidad de una función a trozos
YouTube - Dominio de una función a trozos