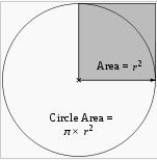
Área del círculo
 |
Autores: Miguel Serrano y Javier Peña
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Área del círculo y aplicaciones
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta sección, se trabajará con el área de un círculo. En las actividades, los alumnos realizarán procedimientos para obtener la fórmula o expresión general del área de un círculo. Luego aplicarán esta fórmula para resolver diferentes situaciones problemáticas, entendiendo que no es el único camino para la resolución de ellas.
Objetivos de las actividades
Que los alumnos:
Interpreten y reconozcan el área del círculo.
Analicen conjeturas sobre relaciones y propiedades geométricas y numéricas.
Analicen, comparen y debatan sobre las distintas situaciones problemáticas y elijan las soluciones, fundamentando el resultado obtenido.
Actividad 1
1) Discutan las siguientes preguntas junto con su docente:
¿Qué es el diámetro y el radio de una circunferencia?
¿Cuál es la expresión general o fórmula para calcular el perímetro de una circunferencia?
¿De dónde sale el número Pi?
¿Cuál es la diferencia entre la circunferencia y el círculo?
Pueden profundizar estos temas en el siguiente link:
Polígonos regulares y círculos.
2) Analicen el siguiente video para comprender cómo se obtiene la fórmula o expresión matemática del área de un círculo.
3) Con base en lo que observaron en el video anterior, analicen y resuelvan las siguientes cuestiones:
a) El área del círculo se deduce sabiendo que la superficie interior de cualquier polígono regular es igual al semiproducto entre la apotema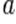 
y el perímetro 
del polígono, es decir:
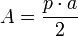
Si consideramos que el perímetro de un círculo es igual a la longitud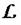 
; de su circunferencia, podemos decir que:
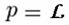
Entonces, ¿a qué es igual la apotema?
b) Utilicen los datos del ítem a) para rescribir la fórmula del área de un círculo colocando los nuevos conceptos.
c) Utilicen el análisis hecho en los ítems anteriores para completar las siguientes igualdades entre las expresiones matemáticas, y expliquen con sus palabras cómo se obtiene el área de un círculo.
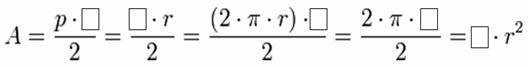
Actividad 2
1) Utilizando la calculadora de sus equipos, calculen el área de un hexágono, un isodecágono y un tetracontágono. Luego, calculen el área del círculo que contiene los polígonos anteriores y compárenla con cada área de estos últimos.
a) ¿Qué resultado se aproxima más al área del círculo?
b) ¿Por qué sucede esto?
Pueden utilizar el link de la Actividad 1 (Polígonos regulares y círculos) para profundizar estos temas.
Actividad de cierre
1) En grupos de dos o tres alumnos, analicen y resuelvan las siguientes situaciones. Utilicen la calculadora científica de sus equipos para realizar todos los cálculos.
a) Calculen el área de la parte sombreada considerando que el radio del círculo mayor mide 8 cm, y el radio de los círculos pequeños, 2 cm.
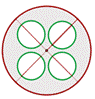
b) En el centro de un parque que tiene forma circular –600 m de radio– hay una fuente, también de forma circular, cuyo radio es de 7 m de radio. Calculen el área de la zona de paseo.
c) En una plaza de forma circular de radio de 250 m se van a poner 7 farolas, cuyas bases son círculos de un 1 m de radio; en el resto de la plaza van a sembrar césped. Calculen el área del césped.
2) Analicen los siguientes videos en lo que se cuentan algunas historias sobre el número Pi:
Universo matemático: 2 historias de Pi 1/5
Universo matemático: 2 historias de Pi 2/5
a) Utilicen el procesador de texto de sus equipos para redactar un resumen de lo analizado.
Enlaces de interés y utilidad para el trabajo
Área de un círculo, en Youtube
Relación entre circunferencia y diámetro, en Youtube