Aplicación de derivadas I
 |
Autor: Rodrigo Weber
Responsable disciplinar: Sebastián
Vera Área disciplinar:
Matemática Temática:
Análisis de funciones, máximos y mínimos. Ceros de una función
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia trabajaremos con la aplicación de derivadas en el marco de la resolución de problemas. A través de las reglas de derivadas, los alumnos podrán plantear diferentes cálculos para resolver distintos problemas y verificar la validez del resultado obtenido, dentro del contexto del problema.
Objetivo de las actividades
Que los alumnos:
Analicen situaciones y resuelvan problemas para comprender la utilidad de las derivadas de una función.
Interpreten la noción de derivadas analítica y gráficamente por medio de ejercicios de aplicación.
Calculen máximos y mínimos de una función utilizando su derivada.
Actividad 1
El instrumento matemático básico para medir la razón de cambio de una función es su derivada. La derivada de una función en un punto representa la razón de cambio instantánea de esa función para ese valor de la variable independiente. En problemas demográficos y económicos, en lugar de derivada se utiliza el término tasa o valor marginal. En problemas de física, química, biología, etc., se suele hablar de velocidad y de rapidez. Mientras que la expresión razón de cambio es utilizada en todas las disciplinas.
1) Visiten los siguientes links y analicen los ejemplos que proponen:
Derivadas, aplicaciones, optimización
Aplicaciones: cálculos máximos y mínimos
a) Luego, grafiquen las funciones que se presentan a continuación utilizando el programa graficador Geogebra, disponible en sus equipos portátiles.
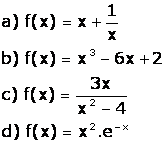 |
b) Calculen las derivadas de las funciones del ítem anterior para encontrar mínimos, máximos y ceros.
Actividad 2
1) Analicen y desarrollen las siguientes situaciones, en las cuales aparece el concepto de derivada:
a) Supongamos que estamos analizando un río en el que ingresan desechos químicos según la siguiente expresión: g(t) = 0 · 2t² + 3 · 8t
g(t) representa la cantidad de deshechos en toneladas que se han vertido al río después de t días.
b) Utilizando el programa Geogebra, instalado en sus equipos portátiles, grafiquen la función g(t).
c) Por medio de una función, expresen la velocidad con que ingresan los desechos químicos al río.
d) Utilicen el programa Geogebra para realizar el gráfico de la función de velocidad hallada en el ítem anterior V(t).
e) ¿Con qué velocidad aumenta la cantidad de deshechos al cabo de una semana?
f) Hallen los máximos y los mínimos de la función V(t).
2) Un grupo de amigos hinchas de Boca que van todos los domingos a la cancha, quiere diseñar una bandera azul, con la franja del medio amarilla, de 14 metros de perímetro. Y quieren que el área de la parte azul sea de 9 m2, pero quieren que la franja amarilla tenga el mayor ancho posible sin alterar los valores antes mencionados.
a) ¿Cuáles deben ser las dimensiones de la bandera para que se cumplan esas condiciones? Utilicen la calculadora científica instalada en sus equipos portátiles para realizar los cálculos necesarios.
b) Hagan un dibujo mostrando posibles medidas de la bandera. Para ello, pueden utilizar algún programa de ilustración.
c) Si el largo tiene que ser mayor que el alto, ¿cómo va a quedar la franja?, ¿vertical u horizontal?
Actividad de cierre
1) En el depósito de la escuela hay 60 m de listones de madera con los que se quiere construir un arenero de forma rectangular. La directora quiere que el arenero tenga la mayor superficie posible para que los chicos lo aprovechen mejor.
a) ¿Qué medidas debe tener el arenero?
Hagan un dibujo mostrando posibles medidas del arenero utilizando un programa ilustrador. Empleen la calculadora científica instalada en sus equipos portátiles para realizar los cálculos necesarios.
2) Discutan con el docente la utilidad que tienen las derivadas para resolver diferentes situaciones.
Enlaces de interés y utilidad para el trabajo
Introducción a las funciones en Geogebra