Foto cedida por la Secretaría de Turismo de la Nación de la República Argentina.

Contenidos

Interpretación de conceptos y relaciones en distintos marcos (geométrico, numérico, algebraico, gráfico) a propósito del trabajo con errores frecuentes de los alumnos.

Propósitos

Gran parte de los conceptos matemáticos pueden intervenir en distintos dominios, en distintos marcos. Sin embargo, posiblemente potenciado por los dispositivos de enseñanza, es habitual que los alumnos no puedan reconocer en otro marco un concepto conocido o que consideren que un mismo concepto funciona de distinto modo según el marco en que se encuentre.

A fin de superar tales dificultades, la siguiente actividad ¹ apunta al trabajo con un error muy arraigado en los alumnos del Tercer Ciclo de la EGB (y que persiste en ciclos superiores) a partir del análisis y de las relaciones de sus significados en los marcos algebraico, geométrico y gráfico.

Desarrollo

En forma muy frecuente observamos que los alumnos realizan simplificaciones como las siguientes:

También es frecuente que los docentes se valgan sólo de contraejemplos a fin de mostrar que tales simplificaciones son incorrectas (por ejemplo, comparar 1/2 y 1/2 + 2/2).

Ahora bien; dicho error puede vincularse con el que cometen los alumnos cuando se les solicita que amplíen un rectángulo de modo tal de obtener otro semejante al primero y agregan o quitan una tira de ancho constante de ambos lados del rectángulo, pues piensan que de tal modo la razón entre las dimensiones permanece constante.

En tal sentido, la siguiente actividad permite una reflexión sobre las relaciones entre tales errores favoreciendo su superación:

Se entrega a los alumnos una fotografía de 4 cm x 2 cm. Queremos ampliarla de modo tal que el lado que mide 4 cm pase a medir 7 cm. ¿Cuánto debe medir el otro lado?

Ante todo debemos resaltar que la elección de la medida del lado de la fotografía ampliada no es casual. En efecto, si solicitamos que el lado que mide 4 cm pase a medir 8 cm no aparece ninguna dificultad pues se trata de duplicar las dimensiones.

En el caso propuesto resulta importante un primer momento de trabajo individual a partir del cual es muy posible que muchos alumnos sugieran que hay que "agregar 3" a ambos lados.

Quizá respondan del siguiente modo: "Si duplicamos todo, tenemos: 4 x 2 = 8; 2 x 2 = 4. Pero el lado mayor tiene que medir 7, que es 8 - 1, por lo que el lado menor tiene que medir 3, que es 4 -1".

Es posible que otros propongan una respuesta correcta razonando de la siguiente manera: "Si a 4 le tengo que sumar 3, a 2 -que es la mitad de cuatro- le tengo que sumar 1,5". Si esta respuesta aparece con mucha fuerza puede sugerirse que consideren que el rectángulo original mide 5 cm x 2 cm, dado que el hecho de que 2 sea la mitad de 4 puede favorecer respuestas como la anterior.

También puede darse que algunos alumnos utilicen otros procedimientos adecuados (regla de tres o el planteo de la proporción correspondiente).

A continuación es conveniente proponer a los alumnos que realicen un sistema de coordenadas cartesianas, ubicando uno de los vértices de los rectángulos en el origen de coordenadas, lo que permitirá mostrar que, para la ampliación correcta, los puntos O, A y B están alineados:

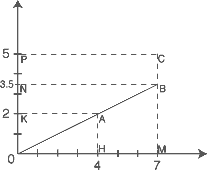
En esta instancia es adecuado volver sobre el error algebraico y proponer la ampliación de una foto cuadrada, lo que permitirá discutir por qué en este caso es pertinente "agregar una faja de ancho constante", del mismo modo que a partir de expresiones como es correcto deducir que es igual y valerse de la siguiente representación:

Sugerencias

A partir de la representación mediante coordenadas cartesianas pueden analizarse las características de las funciones de proporcionalidad directa, la noción de pendiente de una recta y establecer relaciones con la semejanza de figuras planas.

¹.Esta actividad, como así también algunos aspectos considerados en su análisis, han sido tomados de Annie Berté. Matemática dinámica, A-Z Editora, Buenos Aires, 1999.