Movimiento circular uniforme. Modellus
 |
Autor: Hernán Ferrari
Responsable disciplinar: Silvia Blaustein
Área disciplinar: Física
Temática: Movimiento circular uniforme. Software Modellus
Nivel: Secundario, ciclo básico
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
Se denomina movimiento circular a aquel que realiza un cuerpo moviéndose alrededor de una circunferencia. Es uniforme si el ángulo que define la posición del cuerpo, medido desde un sistema de referencia con origen en el centro de la circunferencia, varía en forma proporcional al tiempo.
Se define a la velocidad angular como la variación del ángulo respecto de la variación del tiempo: 
.
De esta forma, las ecuaciones que describen la variación del ángulo son
semejantes a las de la posición en el movimiento rectilíneo uniforme:
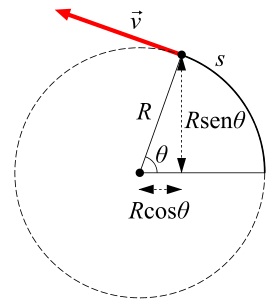
Por su parte, utilizando relaciones trigonométricas se pueden obtener las coordenadas cartesianas de la posición del cuerpo a partir del ángulo y el radio de la circunferencia:
e 
Objetivo de las actividades
Que los alumnos comprendan el movimiento circular uniforme al utilizar la variación angular uniforme en función del tiempo, para que luego, utilizando relaciones trigonométricas, puedan obtener las coordenadas cartesianas del movimiento del cuerpo.
Actividad 1:
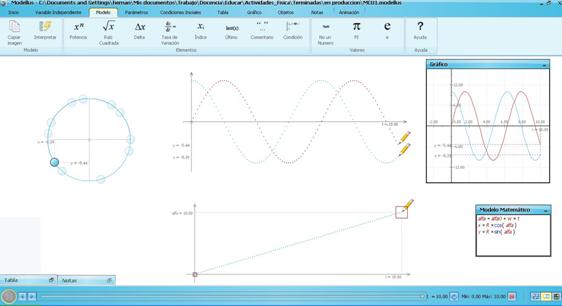
1. Visualizar un movimiento circular uniforme utilizando el software Modellus puede ser muy sencillo si se manejan las relaciones mencionadas en la introducción. De esta forma, en la ventana del “modelo matemático”, se puede escribir:
Para este caso, en el que se trabaja con ángulos, en el menú “Inicio-Sección”, de “Preferencias”, se puede elegir la unidad con la que se medirán los ángulos: grados o radianes. En esta oportunidad, utilizarán radianes y realizarán la visualización para un movimiento con velocidad angular de 1 (radian/segundo) y un ángulo inicial igual a 0.
a) Agreguen una partícula en el entorno de trabajo con las coordenadas x en el horizontal e y en la vertical.
b) En un gráfico, visualicen las coordenadas x e y en función del tiempo.
c) En el entorno de trabajo, agreguen dos lápices con el origen de las coordenadas coincidentes, así se podrán realizar gráficos adicionales al de la ventana “Gráfico”. Para obtener un gráfico similar al de la ventana “Gráfico”, a cada lápiz se le puede asignar el tiempo en el eje horizontal, y en el vertical, la x o la y.
d) Calculen el período de revolución del cuerpo.
e) Asignen un lápiz adicional para mostrar el ángulo en función del tiempo.
f) Escriban un informe detallado de todos los pasos realizados en esta actividad en el procesador de textos de sus equipos portátiles. Incluyan los programas utilizados y los gráficos realizados.
Actividad 2:
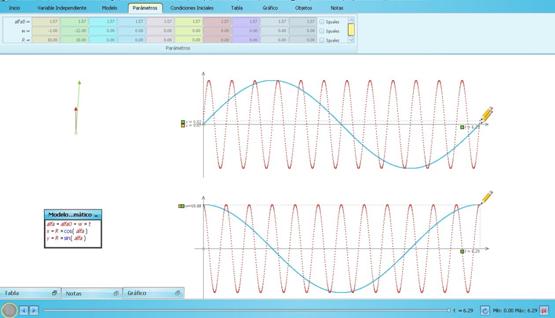
1. Utilizando el software Modellus, resuelvan el problema de encuentro de las agujas de un reloj. Si usan los valores correspondientes para el parámetro velocidad angular, se pueden generar dos movimientos circulares uniformes que simulen el movimiento de las agujas de un reloj. Para ello, calculen la velocidad angular del minutero y de la aguja de las horas.
a) En el Modellus, ingresen dos vectores en el entorno de trabajo para que representen las agujas del reloj.
b) Agreguen dos lápices que grafiquen la coordenada x en función del tiempo, para cada velocidad angular, y lo mismo para la coordenada y.
c) De la tabla de valores, obtengan los instantes de tiempo en los cuales ambas agujas están en el mismo valor de x y de y.
d) Escriban un informe detallado de todos los pasos realizados en esta actividad en el procesador de textos de sus equipos portátiles. Incluyan los programas utilizados y los gráficos realizados.
Actividad 3:
1. Resuelvan el problema de encuentro de las agujas del reloj con el programa Scilab. Utilicen el ángulo de cada aguja en función del tiempo con una precisión de 5 dígitos. Apliquen el método de la bisectriz para alcanzar esta precisión.
a) Usen las funciones seno y coseno del ángulo para obtener el momento en que las posiciones coinciden, o bien la función módulo para que los ángulos del minutero varíen entre 0 y 2p.
b) Realicen un gráfico de los ángulos en función del tiempo.
c) Escriban un informe detallado de todos los pasos realizados en esta actividad en el procesador de textos de sus equipos portátiles. Incluyan los programas utilizados y los gráficos realizados.